a x + b y + c = 0 : Why It Applies to All Straight Lines

June 17, 2017October 6, 2022 / Michael Xue / 1 Comment

In the traditional teaching of Analytical Geometry, the governing equation for a straight line has the following five forms, along with limitations for the first four:

[1] Point-Slope form: $y - y_1 = k (x-x_1)$ where $(x_1, y_1)$ is a point on the line, and $k$ is the slope. The limitation for this form is that it can not represent line perpendicular to the x-axis since it has no slope.

[2] Slope-Intercept form: $y = k x + b$ where $k$ is the slope, $b$ is the intersect the line made on y-axis. Its limitation is that it can not represent line perpendicular to the x-axis.

[3] Two-Point form: $\frac{y-y1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1}$ where $(x_1, y_1), (x_2, y_2)$ are two points on the line. However, this form can represent neither line perpendicular nor parallel to x-axis due to the fact when $x_1 = x_2$ or $y_1 = y_2$ , the form breaks down from dividing by zero.

[4] Point-Intercept form: $\frac{x}{a} + \frac{y}{b} = 1$ where $a, b$ are the intersects the line made on x-axis and y-axis respectively, and $a\neq 0, b\neq0$ . Again, this form can represent neither line perpenticular nor parallel to the x-axis. It does not work for any line that passes the point of origin either.

[5] General form: $a x +b y +c = 0 (a^2+b^2 \neq 0)$ , this form can represent all lines.

Here I am presenting a proof to show [5] is indeed capable of representing all straight lines.

Let us start with an observation:

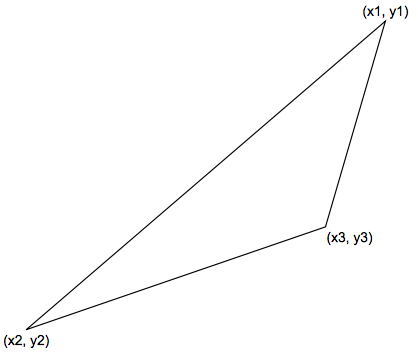
In a rectangular coordinate system, given two distinct points $(x_1, y_1), (x_2, y_2)$ , and any point $(x, y)$ on the line connecting $(x_1, y_1)$ and $(x_2, y_2)$ , the area of triangle with vertices $(x_1, y_1), (x_2, y_2)$ and $(x, y)$ must be zero!

Recall a theorem proved in my blog “Had Heron Known Analytic Geometry“, it means for such $(x_1, y_1), (x_2, y_2)$ and $(x, y)$ ,

$\left|\begin{array}{ccc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x & y & 1 \end{array}\right|= 0$ .

Therefore, we can define the line connecting two distinct points as a set of $(x, y)$ such that the area of the triangle with vertices $(x_1, y_1), (x_2, y_2)$ and $(x, y)$ is zero, mathematically written as

$A \triangleq \{ (x, y) | \left|\begin{array}{ccc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x & y & 1 \end{array}\right|= 0, (x_1-x_2)^2+(y_1-y_2)^2 \neq 0\}$ .

Since $\forall (x, y) \in A$ ,

$\left|\begin{array}{ccc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x & y & 1 \end{array}\right|= x_1 y_2-x y_2-x_2 y_1+x y_1+x_2 y-x_1y =$

$(y-y_1)(x_1-x_2)-(x-x_1)(y_1-y_2)=0\quad\quad\quad\quad(1)$

is an algebraic representation of the line connecting two distinct points $(x_1, y_1)$ and $(x_2, y_2)$ .

When $x_1=x_2$ , (1) becomes

$(x-x_1)(y_1-y_2)=0$ ,

and when $x_1 = x_2, y_1-y_2 \neq 0$ , we have

$x = x_1$ ,

a line perpendicular to the horizontal axis.

When $y_1=y_2$ , (1) becomes

$y = y_1$ ,

a line parallel to the horizontal axis.

Evaluate (1) with $x_2=0, y_2=0$ yields:

$(y-y_1) x_1 -(x-x_1)y_1=0$ .

Collecting terms in (1), and letting

$a=y_1-y_2$ ,

$b=x_2-x_1$ ,

$c=x_1y_2-x_2y_1$ ,

(1) can be expressed as

$ax + by + c = 0$ .

In fact, we can prove the following theorem:

$B \triangleq \{ (x, y) | \exists a, b, a^2+b^2 \neq 0, a x +b y+c=0\} \implies A=B$ .

To prove $A=B$ , we need to show

$\forall (x, y) \in A \implies (x, y) \in B\quad\quad\quad\quad(2)$

$\forall (x, y) \in B \implies (x, y) \in A\quad\quad\quad\quad(3)$

We have already shown (2) by setting the values of $a, b$ and $c$ earlier.

We will prove (3) now:

$\forall (x_1, y_1), (x_2, y_2)$ and $(x, y) \in B$ , we have

$\begin{cases}a x_1 + b y_1 +c =0 \\ a x_2 + b y_2 +c =0 \\ a x + b y+c =0\end{cases}$ .

Written in matrix form,

$\left(\begin{array}{ccc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x & y & 1 \end{array}\right)$ $\left(\begin{array}{rrr} a \\ b \\ c \end{array}\right)= 0$ .

$\left|\begin{array}{ccc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x & y & 1 \end{array}\right| \neq 0$ ,

then by Cramer’s rule,

$\left(\begin{array}{rrr} a \\ b \\ c \end{array}\right)$ is a column vector of zeros,

i.e.,

$a=b=c=0$

which contradicts the fact that

$a,b$ are not all zero.

Hence,

$\left|\begin{array}{ccc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x & y & 1 \end{array}\right| = 0$

which implies:

$(x, y) \in A$ .

The consequence of $A=B$ is that every point $(x, y)$ on a line connecting two distinct points satisfies equation $a x + b y + c =0$ for some $a, b (a^2+b^2\neq 0)$ .

Stated differently,

$a x + b y +c = 0$ where $a, b$ are not all zero is the governing equation of any straight line.

Had Heron Known Analytic Geometry…

June 13, 2017April 7, 2023 / Michael Xue / 4 Comments

In my previous two posts, “An Algebraic Proof of Heron’s Formula” and “An Alternative Derivation of Heron’s Formula,” I proved Heron’s formula for the area of a triangle with three given sides. Based on Heron’s formula, we can now prove a theorem concerning the area of any triangle in a rectangle coordinate system, namely,

The area of a triangle with vertices at $(x_1, y_1), (x_2, y_2), (x_3, y_3)$ in a rectangle coordinate system can be expressed as

$|\frac{1}{2}D|\quad\quad\quad\quad\quad\quad\quad\quad\quad(1)$

where $D$ is the determinant of matrix:

$\begin{pmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{pmatrix}$

I offer the following proof:

Screen Shot 2017-06-14 at 1.02.37 PM.png

Fig. 1

By Heron’s formula, the area of triangle in Fig. 1

$A=\sqrt{s (s-a) (s-b) (s-c)}\quad\quad\quad\quad\quad(2)$

where $a, b, c$ are three sides of the triangle and, $s=(a+b+c)/2$ .

Therefore,

$A^2=s(s-a)(s-b)(s-c).$

where

$a^2=(x_2-x_3)^2+(y_2-y_3)^2,$

$b^2=(x_1-x_3)^2+(y_1-y_3)^2,$

$c^2=(x_1-x_2)^2+(y_1-y_2)^2.$

Let $B=|\frac{1}{2} D|$ , we have

$B^2 ={|\frac{1}{2} D|}^2=(\frac{1}{2}D)^2.$

Compute $A^2-B^2$ using Omega CAS Explorer (see Fig. 2) , the result shows

$A^2-B^2=0.$

Screen Shot 2017-06-13 at 9.21.21 PM.png

Fig. 2

Since $A> 0, B\geq 0$ implies

$A+B >0,$

$A^2-B^2=(A-B)(A+B)=0$ implies

$A-B=0$ ,

i.e.,

$A = B.$

Hence, (1) and (2) are equivalent.

I would like to learn any other alternative proof.

Higham’s Parametric Curve

June 9, 2017July 10, 2017 / Michael Xue / 1 Comment

Screen Shot 2017-06-10 at 11.02.26 AM.png

Fig. 1

The parametric curve (see Fig. 1) has always intrigued me. It was to my delight to finally find its equations from “MATLAB guide” written by the Highams:

$x = \int\limits_{0}^{t} \sin {\omega^2}\; d\omega$

$y = \int\limits_{0}^{t} \cos {\omega^2}\; d\omega$

Below is the curve plotted by Omega CAS Explorer:

Screen Shot 2017-06-10 at 12.43.19 PM.png

Fig. 2

After several failed trials, I realized that ‘nticks’ must be provided in ‘plot2d’ in order to produced the image correctly.

Next, I tried ‘draw2d’ function (see Fig. 3), but the tics and numbers are too close to the image of the curve.

Screen Shot 2017-06-10 at 12.36.10 PM.png

Fig. 3

To better position the image, I specified ‘xrange’ and ‘yrange’ to put more space between the image and the tics and numbers. Cropping the resulting image to obtain the Fig. 1 at the top of this post.

Screen Shot 2017-06-10 at 12.39.31 PM