Deriving Two Inverse Functions

July 22, 2021October 10, 2022 / Michael Xue / 3 Comments

In “Instrumental Flying“, we defined function $y=\mathrm{arcsinh}(x)$ as

$\{(x, y) | x = \frac{e^y-e^{-y}}{2}\}.\quad\quad\quad(1)$

From $x = \frac{e^y-e^{-y}}{2}$ , we obtain

$(e^y)^2-2x\cdot e^y-1=0.$

It means either $e^y = x-\sqrt{x^2+1}$ or $e^y = x+\sqrt{x^2+1}.$

But $e^y = x-\sqrt{x^2+1}$ suggests $e^y < 0$ (see Exercise-1), contradicts the fact that $\forall t \in R, e^t > 0$ (see “Two Peas in a Pod, Part 2“).

Therefore,

$e^y = x+\sqrt{x^2+1} \implies y = \log(x + \sqrt{x^2+1}).$

i.e.,

$\mathrm{arcsinh}(x) = \log(x + \sqrt{x^2+1}), \;\;x \in (-\infty, +\infty).$

We also defined a non-negative valued function $y = \mathrm{arccosh}(x)$ :

$\{(x, y) | x = \frac{e^y + e^{-y}}{2}, y \ge 0\}.\quad\quad\quad(2)$

Simplifying $x=\frac{e^y+e^{-y}}{2}$ yields

$(e^y)^2-2x\cdot e^y+1=0.$

It follows that either $e^y = x-\sqrt{x^2-1}$ or $e^y=x+\sqrt{x^2-1}.$

For both expressions’ right-hand side to be valid requires that $x \ge 1$ . However, when $x = 2$ ,

$e^y = x-\sqrt{x^2-1} = 2 - \sqrt{3} < 1$

suggests that $y < 0$ (see Exercise-2,3), contradicts (2).

Hence,

$e^y = x+\sqrt{x^2-1} \implies y = \log(x+\sqrt{x^2-1}).$

i.e.,

$\mathrm{arccosh}(x) = \log(x+\sqrt{x^2-1}), \;\;x \in [1, +\infty).$

Beltrami’s Identity

July 19, 2021October 7, 2022 / Michael Xue / Leave a comment

The Beltrami’s identity

$F - y' \frac{\partial F}{\partial y'} = C$

where $C$ is a constant, is a reduced form of Euler-Lagrange equation for the special case when $F$ does not dependent explicitly on $x$ .

For $F = F(y, y')$ ,

$\frac{dF}{dx} = \frac{\partial F}{\partial y} y' + \frac{\partial F}{\partial y'} y''.\quad\quad\quad(1)$

From Euler-Lagrange equation

$\frac{\partial F}{\partial y} - \frac{d}{dx}(\frac{\partial F}{\partial y'}) = 0,$

we have

$\frac{\partial F}{\partial y} = \frac{d}{dx}(\frac{\partial F}{\partial y'}).\quad\quad\quad(2)$

Substituting (2) into (1) gives

$\frac{dF}{dx} = \frac{d}{dx}(\frac{\partial F}{\partial y'}) y' + \frac{\partial F}{\partial y'} y''.\quad\quad\quad(3)$

Consequently, when (3) is expressed as

$\frac{dF}{dx} = \frac{d}{dx}(\frac{\partial F}{\partial y'}) y' + \frac{\partial F}{\partial y'} \frac{dy'}{dx},$

it becomes clear that

$\frac{dF}{dx} = \frac{d}{dx}(\frac{\partial F}{\partial y'}y').$

Therefore,

$\frac{d}{dx}(F-\frac{\partial F}{\partial y'}y') = 0.$

i.e.,

$F - y' \frac{\partial F}{\partial y'} = C.$

In “A Relentless Pursuit”, we derived differential equation

$\frac{dy}{dx} = \frac{\sqrt{y^2-C_1^2}}{\pm C_1}\quad\quad\quad(4)$

from Euler-Lagrange equation without taking advantage of the fact that $F=y\sqrt{1+(y')^2}$ has no explicit dependency on $x$ . The derivation was mostly done by a CAS.

Let’s derive (4) from Beltrami’s Identity. This time, we will not use CAS.

For $F=y\sqrt{1+(y')^2}$ , the Beltrami’s Identity is

$y\sqrt{1+(y')^2} - y'\cdot\left(y\cdot\frac{1}{2}\frac{2y'}{\sqrt{1+(y')^2}}\right) = C.$

It simplifies to

$\frac{y}{\sqrt{1+(y')^2}} = C.$

Further simplification yields

$C^2(y')^2 = y^2-C^2.$

For $C \ne 0$ ,

$(y')^2 = \frac{y^2-C^2}{C^2}.$

Therefore,

$\frac{dy}{dx} = \pm \sqrt{\frac{y^2-C^2}{C^2}}=\frac{\sqrt{y^2-C^2}}{\pm C}.$

Prequel to “A Relentless Pursuit”

July 15, 2021October 6, 2022 / Michael Xue / Leave a comment

Fig. 1

Illustrated in Fig. 2 are two circular hoops of unit radius, centered on a common x-axis and a distance 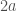$2a$ apart. There is also a soap films extends between the two hoops, taking the form of a surface of revolution about the x-axis. If gravity is negligible, the film takes up a state of stable, equilibrium in which its surface area is a minimum.

Fig. 2

Our problem is to find the function 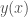$y(x)$ , satisfying the boundary conditions

$y(-a) = y(a) = 1,\quad\quad\quad(1)$

which makes the surface area

$A=2\pi\displaystyle\int\limits_{-a}^{a}y\sqrt{1+(y')^2}\;dx\quad\quad\quad(2)$

a minimum.

Let

$F(x,y, y') = 2\pi y \sqrt{1+(y')^2}.$

We have

$\frac{\partial F}{\partial y} = 2\pi \sqrt{1+(y')^2}$

and

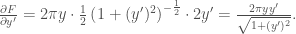
$\frac{\partial F}{\partial y'} = 2 \pi y \cdot\frac{1}{2}\left(1+(y')^2\right)^{-\frac{1}{2}}\cdot 2y'=\frac{2 \pi y y'}{\sqrt{1+(y')^2}}.$

The Euler-Lagrange equation

$\frac{\partial F}{\partial y} - \frac{d}{dx}\left(\frac{\partial F}{\partial y'}\right) = 0$

becomes

$\sqrt{1+(y')^2} - \frac{d}{dx}\left(\frac{y y'}{\sqrt{1+(y')^2}}\right) = 0.$

Fig. 3

Using Omega CAS Explorer (see Fig. 3), it can be simplified to:

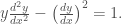
$y \frac{d^2 y}{dx^2}- \left(\frac{dy}{dx}\right)^2=1.$

This is the differential equation solved in “A Relentless Pursuit” whose solution is

$y = C_1\cdot \cosh(\frac{x+C_2}{C_1}).$

We must then find 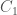$C_1$ and $C_2$ subject to the boundary condition (1), i.e.,

$C_1\cdot \cosh(\frac{a+C_2}{C_1}) = C_1\cdot\cosh(\frac{-a+C_2}{C_1})\implies \cosh(\frac{a+C_2}{C_1}) = \cosh(\frac{-a+C_2}{C_1}).$

The fact that 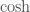$\cosh$ is an even function implies either

$a+C_2 = -a+C_2\quad\quad\quad(3)$

$a+C_2 = -(-a+C_2).\quad\quad\quad(4)$

While (3) is clearly false since it claims for all $a >0, a = -a$ , (4) gives

$C_2=0.$

And so, the solution to boundary-value problem

$\begin{cases} y \frac{d^2 y}{dx^2}- \left(\frac{dy}{dx}\right)^2=1,\\ y(-a)=y(a)=1\end{cases}\quad\quad\quad(5)$

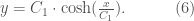
$y = C_1\cdot \cosh(\frac{x}{C_1}).\quad\quad\quad(6)$

To determine 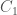$C_1$ , we deduce the following equation from the boundary conditions that $y=1$ at $x=\pm a:$

$C_1\cdot \cosh(\frac{a}{C_1}) = 1.\quad\quad\quad(7)$

This is a transcendental equation for 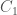$C_1$ that can not be solved explicitly. Nonetheless, we can examine it qualitatively.

Let

$\mu = \frac{a}{C_1}$

and express (7) as

$\cosh(\mu) = \frac{\mu}{a}.\quad\quad\quad(8)$

Fig. 4

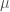A plot of (8)’s two sides in Fig. 4 shows that for sufficient small $a$ , the curves $z = \cosh(\mu)$ and $z = \frac{\mu}{a}$ will intersect. However, as $a$ increases, $z=\frac{\mu}{a}$ , a line whose slope is $\frac{1}{a}$ rotates clockwise towards $\mu$ -axis. The curves will not intersect if $a$ is too large. The critical case is when $a=a^*$ , the curves touch at a single point, so that

$\cosh(\mu) = \frac{\mu}{a^*}\quad\quad\quad(9)$

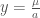and $y=\frac{\mu}{a}$ is the tangent line of 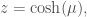$z=\cosh(\mu),$ i.e.,

$\sinh(\mu) = \frac{1}{a^*}.\quad\quad\quad(10)$

Dividing (9) by (10) yields

$\coth(\mu) = \mu. \quad\quad\quad(11)$

What the mathematical model (5) predicts then is, as we gradually move the rings apart, the soap film breaks when the distance between the two rings reaches 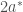$2a^*$ , and for $a > a^*$ , there is no more soap film surface connects the two rings. This is confirmed by an experiment (see Fig. 1).

We compute the value of $a^*$ , the maximum value of $a$ that supports a minimum area soap film surface as follows.

Fig. 5

Solving (11) for 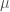$\mu$ numerically (see Fig. 5), we obtain

$\mu = 1.1997.$

By (10), the corresponding value of

$a^* = \frac{1}{\sinh(\mu)} = \frac{1}{\sinh(1.1997)} = 0.6627$ .

We also compute the surface area of the soap film from (2) and (6) (see Fig. 6). Namely,

$A = 2\pi \displaystyle\int\limits_{-a}^{a} C_1 \cosh\left(\frac{x}{C_1}\right) \sqrt{1+\left(\frac{d}{dx}C_1\cosh\left(\frac{x}{C_1}\right)\right)^2}\;dx = \pi C_1^2\left(\sinh\left(\frac{2a}{C_1}\right) + \frac{2a}{C_1}\right).$

Fig. 6

Exercise-1 Given 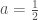$a=\frac{1}{2}$ , solve (7) numerically for $C_1.$

Exercise-2 Without using a CAS, find the surface area of the soap film from (2) and (6).

An Epilogue to “A Relentless Pursuit”

July 1, 2021October 6, 2022 / Michael Xue / Leave a comment

Let

$p=\frac{dy}{dx},$

differential equation (1) in “A Relentless Pursuit” can be expressed as

$\frac{dp}{dy}-\frac{1}{y}p = \frac{1}{y}p^{-1}.$

This is Bernoulli’s equation

$\frac{dp}{dy} + f(y) p = g(y) p^{\alpha}$

with $f(y) = -\frac{1}{y}, g(y) = \frac{1}{y}$ and $\alpha = -1$ (see “Meeting Mr. Bernoulli“).

Hence,

$p^{1-\alpha} = e^{(\alpha-1)\displaystyle\int f(y)\;dy}\left((1-\alpha)\displaystyle\int e^{-(\alpha-1)\displaystyle\int f(y)\;dy} g(y)\;dy + C\right).\quad\quad\quad(1)$

Substitute $f(y), g(y)$ and $\alpha$ into (1) gives

$p^{1-(-1)} = e^{(-1-1)\displaystyle\int -\frac{1}{y}\; dy}\left((1-(-1))\displaystyle\int e^{-(-1-1)\displaystyle\int -\frac{1}{y}\;dy}\frac{1}{y}\;dy+C\right).$