An isosceles right triangle ABC is depicted blow where M is the midpoint of the hypotenuse AB, P is any point on AB, PE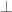 AC and PF
AC and PF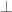 BC. Show that MF
BC. Show that MF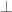 ME.
ME.
Consider the triangle within a coordinate system, as illustrated in Fig. 1:
Fig. 1  and
and 
Let 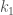 and
and 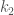 denotes the slopes of
denotes the slopes of  and
and  , respectively. We express them as follows:
, respectively. We express them as follows:
 and
and  .
.
This means that






Certainly, this holds true for  as it lies on the hypotenuse
as it lies on the hypotenuse 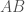 , which can be represented by the equation
, which can be represented by the equation

Now, let’s provide a step-by-step proof:
 lies on the hypotenuse of
lies on the hypotenuse of 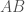







 .
.
An alternative proof is:



 .
.
From the right triangle  , we observe that
, we observe that

Therefore,

This implies that  is a right triangle. i.e.,
is a right triangle. i.e.,
 .
.
Treating  and
and  as vectors and utilizing the vector equation of line
as vectors and utilizing the vector equation of line 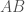 , we have yet another proof:
, we have yet another proof:
Fig. 2
Let
 and
and 
The inner product of  and
and 

The vector equation of the line 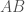

is

Thus, combining the components:

Submitting  into (2) gives
into (2) gives

Let’s also prove it synthetically.
Fig. 3 
Given

and

Similarly,

It follows that
 and
and  are right triangles
are right triangles

Thus,

Consequently,



See also “Deriving the vector equation of line”.

and
are two non-zero vectors, and
is defined as
, then on one hand,





















