Generating an integral representation of Zeta(3)

April 28, 2024April 29, 2024 / Michael Xue / Leave a comment

$\displaystyle \int\limits_{0}^{1}\int\limits_{0}^{1}\frac{x^{\beta} y^{\beta}}{1-xy}\;dx\;dy = \sum\limits_{i=1}^{\infty}\frac{1}{(i+\beta)^2}$

(see (3) in A Page in my Notebook [2])

$\displaystyle \implies \frac{d}{d\beta} \int\limits_{0}^{1}\int\limits_{0}^{1}\frac{x^{\beta} y^{\beta}}{1-xy}\;dx\;dy = \frac{d}{d\beta}\sum\limits_{i=1}^{\infty}\frac{1}{(i+\beta)^2}$

$\displaystyle \implies \int\limits_{0}^{1}\int\limits_{0}^{1}\frac{d}{d\beta}\left(\frac{(x y)^{\beta}}{1-xy}\right)\;dx\;dy = \frac{d}{d\beta}\sum\limits_{i=1}^{\infty}\frac{1}{(i+\beta)^2}$

$\displaystyle \implies \int\limits_{0}^{1}\int\limits_{0}^{1}\frac{(x y)^{\beta} \log(xy)}{1-xy}\;dx\;dy = -2 \sum\limits_{i=1}^{\infty}\frac{1}{(i+\beta)^3}$

$\displaystyle \overset{\beta = 0}{\implies} \int\limits_{0}^{1}\int\limits_{0}^{1}\frac{\log(xy)}{1-xy}\;dx\;dy = -2 \sum\limits_{i=1}^{\infty}\frac{1}{i^3}$

$\displaystyle \implies \int\limits_{0}^{1}\int\limits_{0}^{1}\frac{\log(x)}{1-xy}\;dx\;dy + \int\limits_{0}^{1}\int\limits_{0}^{1}\frac{\log(y)}{1-xy}\;dx\;dy= -2 \sum\limits_{i=1}^{\infty}\frac{1}{i^3}$

$\displaystyle \implies 2 \int\limits_{0}^{1}\int\limits_{0}^{1}\frac{\log(x)}{1-xy}\;dx\;dy = -2 \sum\limits_{i=1}^{\infty}\frac{1}{i^3}$

That is,

$\displaystyle \zeta(3) = \sum\limits_{i=1}^{\infty}\frac{1}{i^3} = -\int\limits_{0}^{1}\int\limits_{0}^{1}\frac{\log(x)}{1-xy}\;dx\;dy$

Exercise-1 Show that $\displaystyle \int\limits_{0}^{1}\int\limits_{0}^{1}\int\limits_{0}^{1}\frac{1}{1-xyz} dx dy dz= -\int\limits_{0}^{1}\int\limits_{0}^{1}\frac{\log(x)}{1-xy}\;dx\;dy$

Exercise-2 Generating $\displaystyle \zeta(4), \zeta(5), \zeta(6)....$

A Page in My Notebook [2]

April 26, 2024April 29, 2024 / Michael Xue / Leave a comment

$\displaystyle \int\limits_{0}^{1}\int\limits_{0}^{1}\frac{1}{1-xy}\;dx\;dy$

$\frac{1}{1-xy} = 1+xy +(xy)^2 + (xy)^3+(xy)^4 + ... = \sum\limits_{i=0}^{\infty}(xy)^i$

$\displaystyle = \int\limits_{0}^{1}\int\limits_{0}^{1}\sum\limits_{i=0}^{\infty}(xy)^i\;dx\;dy = \int \limits_{0}^{1} \sum\limits_{i=0}^{\infty}\int\limits_{0}^{1} (xy)^i \;dx \;dy$

$\displaystyle = \int\limits_{0}^{1}\sum\limits_{i=0}^{\infty}y^i\int\limits_{0}^{1} x^i \;dx \; dy= \int\limits_{0}^{1}\sum\limits_{i=0}^{\infty}y^i \frac{x^{i+1}}{i+1} \bigg|_{0}^{1}\; dy = \sum\limits_{i=0}^{\infty} \int\limits_{0}^{1} \frac{y^i}{i+1}\; dy= \sum\limits_{i=0}^{\infty}\frac{y^{i+1}}{(i+1)^2}\bigg|_{0}^{1}$

$\displaystyle = \sum\limits_{i=0}^{\infty}\frac{1}{(i+1)^2} = \sum\limits_{i=1}^{\infty}\frac{1}{i^2}.$

It follows that by An Analytic Proof of the Extraordinary Euler Sum,

$\displaystyle \int\limits_{0}^{1}\int\limits_{0}^{1}\frac{1}{1-xy}\;dx\;dy = \frac{\pi^2}{6}\quad\quad\quad(1)$

Similarly,

$\displaystyle \int\limits_{0}^{1} \int\limits_{0}^{1}\frac{1}{1-(xy)^2}\;dx\;dy = \int\limits_{0}^{1} \int\limits_{0}^{1}\sum\limits_{i=0}^{\infty}(xy)^{2i}\;dx\;dy=\int\limits_{0}^{1}\sum\limits_{i=0}^{\infty}y^{2i}\int\limits_{0}^{1}x^{2i}\;dx\;dy$

$\displaystyle \int\limits_{0}^{1}\sum\limits_{i=0}^{\infty}y^{2i}\frac{1}{2i+1}\;dy = \sum\limits_{i=0}^{\infty}\int\limits_{0}^{1}y^{2i}\frac{1}{2i+1}\;dy = \sum\limits_{i=0}^{\infty}\frac{1}{(2i+1)^2} = \frac{\pi^2}{8}\quad\quad\quad(2)$

It is also true that

$\displaystyle \int\limits_{0}^{1}\int\limits_{0}^{1}\frac{x^{\beta} y^{\beta}}{1-xy}\;dx\;dy = \sum\limits_{i=1}^{\infty}\frac{1}{(i+\beta)^2}\quad\quad\quad(3)$

We demonstrate (3) through the following steps:

$\displaystyle \int\limits_{0}^{1}\int\limits_{0}^{1}\frac{x^{\beta} y^{\beta}}{1-xy}\;dx\;dy = \int\limits_{0}^{1} \int\limits_{0}^{1} x^\beta y^\beta \sum\limits_{i=0}^{\infty}(xy)^i\;dx\;dy = \int\limits_{0}^{1}\sum\limits_{i=0}^{\infty}y^{i+\beta}\int\limits_{0}^{1} x^{i+\beta}\; dx\;dy$

$\displaystyle = \int\limits_{0}^{1}\sum\limits_{i=0}^{\infty}y^{i+\beta}\frac{1}{i+\beta+1}\;dy = \sum\limits_{i=0}^{\infty} \int\limits_{0}^{1} y^{i+\beta}\frac{1}{i+\beta+1}\;dy = \sum\limits_{i=0}^{\infty} \frac{1}{(i+\beta+1)^2}$

$\displaystyle = \sum\limits_{i=1}^{\infty} \frac{1}{(i+\beta)^2}.$

Exercise-1 Show that $\displaystyle \int\limits_{0}^{1}\int\limits_{0}^{1}\frac{1}{1+xy}\;dx\;dy = \frac{\pi^2}{12}.$

(If you are considering rewrite $\frac{1}{1+xy}$ as $\frac{1}{1-(-xy)}$ , don’t! Use (1) and (2) instead)

Exercise-2 Is $\displaystyle \sum\limits_{i=0}^{\infty}\frac{(-1)^i}{(i+1)^2} = \frac{\pi^2}{12}$ ?

A Page in My Notebook [1]

April 11, 2024April 26, 2024 / Michael Xue / Leave a comment

$\displaystyle \int\limits_{0}^{1}\frac{\log(1+x)}{1+x^2}\;dx$

$\displaystyle \phi(t) = \frac{1-t}{1+t} \implies \phi'(t) = \frac{-2}{(1+t)^2}$

$\frac{1-t}{1+t}=0 \implies t=1, \quad \frac{1-t}{1+t}=1 \implies t=0$

$\displaystyle = \int\limits_{1}^{0}\frac{\log\left(1+\frac{1-t}{1+t}\right)}{1+\left(\frac{1-t}{1+t}\right)^2}\cdot\frac{-2}{(1+t)^2}\;dt$

$\displaystyle = ...$

$\displaystyle =\int\limits_{1}^{0}\frac{-\log(2)}{1+t^2}\;dt + \int\limits_{1}^{0}\frac{\log(1+t)}{1+t^2}\;dt$

$\displaystyle =\int\limits_{0}^{1}\frac{\log(2)}{1+t^2}\;dt - \int\limits_{0}^{1}\frac{\log(1+t)}{1+t^2}\;dt.$

That is,

$\displaystyle \underline{\int\limits_{0}^{1}\frac{\log(1+x)}{1+x^2}\;dx} = \int\limits_{0}^{1}\frac{\log(2)}{1+t^2}\;dt-\underline{\int\limits_{0}^{1}\frac{\log(1+t)}{1+t^2}\;dt}$

$\underline{\int\limits_{0}^{1}\frac{\log(1+x)}{1+x^2}\;dx} = \underline{\int\limits_{0}^{1}\frac{\log(1+t)}{1+t^2}\;dt}\quad\quad\quad(1)$

$\displaystyle \implies \underline{\int\limits_{0}^{1}\frac{\log(1+t)}{1+t^2}\;dt} = \int\limits_{0}^{1}\frac{\log(2)}{1+t^2}\;dt-\underline{\int\limits_{0}^{1}\frac{\log(1+t)}{1+t^2}\;dt}$

$\displaystyle \implies 2\underline{\int\limits_{0}^{1}\frac{\log(1+t)}{1+t^2}\;dt} = \log(2)\int\limits_{0}^{1}\frac{1}{1+t^2}\;dt.$

And so,

$\displaystyle \int\limits_{0}^{1}\frac{\log(1+t)}{1+t^2}\;dt = \frac{\log(2)}{2}\int\limits_{0}^{1}\frac{1}{1+t^2}\;dt = \frac{\log(2)}{2}\arctan(t)\bigg|_{0}^{1} \overset{\arctan(1)=\frac{\pi}{4}}{=} \frac{\pi}{8}\log(2).$

By (1),

$\displaystyle \int\limits_{0}^{1}\frac{\log(1+x)}{1+x^2}\;dx = \frac{\pi}{8}\log(2).$

Introducing Feynman’s Integral Method (MAA Meeting, Spring 2024)

April 3, 2024April 29, 2024 / Michael Xue / Leave a comment

Introducing Feynman’s Integral Method

Michael Xue

Indiana Section MAA Spring 2024 MEETING
Marian University – Indianapolis
April 5-6, 2024

“The first principle is that you must not fool yourself and you are the easiest person to fool.”

— Richard Feynman

This is one of my favorite quotes because it speaks to the importance of humility when approaching mathematics and science. To me, it means not being constrained by my existing knowledge or beliefs, nor by previous learning or observations of others’ methods. It’s about freeing my mind to view things from a entirely new perspective.

Feynman’s Integral Method

Leibniz : “ $\displaystyle \frac{d}{d\beta}\int\limits_{a}^{b}f(x, \beta) \;dx = \int\limits_{a}^{b}\frac{\partial}{\partial\beta}f(x, \beta)\;dx$ ”

Feynman: “To evaluate hard $\displaystyle \int\limits_{a}^{b} f(x)\;dx,$ differentiate under the integral sign!”

Feynman’s integral method is a potent mathematical technique developed to simplify complex integrals, often transforming them into more manageable forms. This method, pioneered by Richard Feynman, effectively brought Leibniz’s theorem into practical use, showcasing its real-world applicability in solving intricate mathematical problems.

Two algorithms implementing Feynman’s Integral method

Algorithm #1 Reducing $\displaystyle \int\limits_{a}^{b} f(x)\;dx$

Algorithm #2 Generating $\displaystyle \int\limits_{a}^{b}f(x)\;dx$ from a known definite integral

Like many other mathematicians and physicists, I’ve extensively experimented with Feynman’s method in solving numerous problems. Through a gradual, inductive approach, I’ve discerned patterns that allowed me to synthesize these into two efficient algorithms. Today’s talk will focus on these algorithms, demonstrating their effectiveness in implementing Feynman’s method. I’ll provide multiple examples to illustrate how these algorithms can be used to solve a wide range of mathematical problems.

Example-1

Evaluate $\displaystyle I=\int\limits_{0}^{1}\frac{x-1}{\log(x)}\;dx$

$\displaystyle J(\beta) = \int\limits_{0}^{1}\frac{x^\beta-1}{\log(x)}\;dx \implies J(1)=I, J(0)=0$

$\displaystyle \frac{d}{d\beta}J(\beta) = \int\limits_{0}^{1}\frac{\partial}{\partial \beta}\left(\frac{x^\beta-1}{\log(x)}\right)\;dx = \int\limits_{0}^{1}x^\beta\;dx=\frac{x^{\beta+1}}{\beta+1}\bigg|_{0}^{1}=\frac{1}{\beta+1}$

$\displaystyle \int\limits_{0}^{1}\frac{d}{d\beta}J(\beta)\;d\beta = \int\limits_{0}^{1}\frac{1}{\beta+1}\;d\beta \implies J(1)-J(0) = \log(\beta+1)\bigg|_{0}^{1} = \log(2)$

$\displaystyle \overset{J(1)=I, J(0)=0}{\implies} I = \log(2)$

Example-2

Evaluate $\displaystyle I = \int\limits_{0}^{\infty} e^{-x^2}\;dx$

$\displaystyle J(\beta) = \int\limits_{0}^{\infty}\frac{e^{-\beta^2(x^2+1)}}{1+x^2}\;dx \implies J(0)=\arctan(x)\bigg|_{0}^{\infty}=\frac{\pi}{2}, \quad \underline{J(\infty)=0}$

$\displaystyle \frac{d}{d\beta}J(\beta) = \int\limits_{0}^{\infty}\frac{\partial}{\partial \beta}\left(\frac{e^{-\beta^2(1+x^2)}}{1+x^2}\right)\;dx = -2\beta e^{-\beta^2}\int\limits_{0}^{\infty}e^{-\beta^2x^2}\;dx$

$\displaystyle \overset{\phi(t)=\frac{t}{\beta}, \phi'(t)\frac{1}{\beta}}{=}-2e^{-\beta^2}\int\limits_{0}^{\infty}e^{-t^2}\;dt = -2e^{-\beta^2}I$

$\displaystyle \int\limits_{0}^{\infty}\frac{d}{d\beta}J(\beta)\;d\beta=\int\limits_{0}^{\infty}-2e^{-\beta^2}I\; d\beta = -2I\int\limits_{0}^{\infty}e^{-\beta^2}\;d\beta = -2 I \cdot I = -2I^2$

$\displaystyle J(\infty) - J(0) = -2I^2 \overset{J(0)=\frac{\pi}{2}, J(\infty)=0}{\implies} 0 - \frac{\pi}{2}=-2I^2 \implies I=\frac{\sqrt{\pi}}{2}$

Example-3

Evaluate $\displaystyle \int\limits_{0}^{1}\log(x)\;dx$

For $\displaystyle \beta \ge 0, \int\limits_{0}^{1}x^\beta\;dx = \frac{1}{\beta+1} \implies \frac{d}{d\beta}\int\limits_{0}^{1}x^\beta\;dx = \frac{d}{d\beta}\left(\frac{1}{\beta+1}\right)$

$\displaystyle \implies \int\limits_{0}^{1}\frac{\partial}{\partial \beta}x^\beta\;dx = \frac{-1}{(\beta+1)^2}\implies \int\limits_{0}^{1}x^\beta\log(x)\;dx = \frac{-1}{(\beta+1)^2}$

$\displaystyle \overset{\beta=0}{\implies} \int\limits_{0}^{1}\log(x)\;dx = -1$

$\displaystyle \int\limits_{0}^{1}\log(x)\;dx = \int\limits_{0}^{1}\frac{d}{dx}x\cdot\log(x)\;dx = \underbrace{x\log(x)\bigg|_{0}^{1}}_{\blacksquare}-\int\limits_{0}^{1}\;dx$

Using traditional methods, you often encounter problematic forms like 0 multiplied by infinity. However, Feynman’s method effectively circumvents this issue without the need to invoke L’Hôpital’s rule.

Example-4

Given $\displaystyle \int\limits_{-\infty}^{\infty}\frac{e^{2x}}{a e^{3x}+b}\;dx = \frac{2\pi}{3\sqrt{3}a^\frac{2}{3} b^\frac{1}{3}}, a, b >0,$ find $\displaystyle \int\limits_{-\infty}^{\infty}\frac{e^{2x}}{(e^{3x}+1)^2}\;dx.$

$\displaystyle \frac{d}{db}\int\limits_{-\infty}^{\infty}\frac{e^{2x}}{a e^{3x}+b}\;dx = \frac{d}{db}\left(\frac{2\pi}{3\sqrt{3}a^\frac{2}{3} b^\frac{1}{3}}\right) \implies \int\limits_{-\infty}^{\infty}-\frac{e^{2x}}{(a e^{3x}+b)^2}\;dx = -\frac{2\pi}{3^\frac{5}{2}a^\frac{2}{3}b^\frac{4}{3}}$

$\displaystyle \overset{a=1, b=1}{\implies}\int\limits_{-\infty}^{\infty}\frac{e^{2x}}{(e^{3x}+1)^2}\;dx=\frac{2\pi}{9\sqrt{3}}$

While preparing for this talk last weekend, I developed an example and here is an abbreviated version of the proof to highlight the key steps.

Example-5

Prove $\displaystyle 1 + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + ... = \frac{\pi^2}{6}\quad\quad(\star)$

Since $\displaystyle\sum\limits_{i=1}\frac{1}{i^2}=\sum\limits_{i=1}\frac{1}{(2i)^2} + \sum\limits_{i=0}\frac{1}{(2i+1)^2}\implies \sum\limits_{i=0}^{\infty}\frac{1}{(2i+1)^2} = \frac{3}{4}\sum\limits_{i=1}^{\infty}\frac{1}{i^2},$

to prove $(\star)$ , it suffices to demonstrate that

$\displaystyle \sum\limits_{i=0}^{\infty}\frac{1}{(2i+1)^2} = \frac{\pi^2}{8}$

$\displaystyle I = \int\limits_{0}^{\infty}\frac{\arctan(x)}{1+x^2}\;dx, \quad J(\beta) =\int\limits_{0} ^{\infty}\frac{\arctan(\beta x)}{1+x^2}\;dx$

$\displaystyle \implies J(1) = I =\frac{1}{2}\arctan^2(x)\bigg|_{0}^{\infty} = \frac{\pi^2}{8}, \quad J(0)=0$

$\displaystyle \frac{d}{d\beta}J(\beta) = ... = \int\limits_{0}^{\infty}\frac{x}{(1+x^2)(\beta^2 x^2+1)}\;dx \implies \int\limits_{0}^{1}\frac{d}{d\beta}J(\beta)d\beta=\int\limits_{0}^{1}\int\limits_{0}^{\infty}\frac{x}{(1+x^2)(\beta^2 x^2+1)}\;dx d\beta$

$\displaystyle \implies J(1)-J(0) = \int\limits_{0}^{1}\int\limits_{0}^{\infty}\frac{x}{(1+x^2)(\beta^2 x^2+1)}\;dx\;d\beta=...=\int\limits_{0}^{1}\frac{\log(\beta)}{\beta^2-1}\;d\beta = ...$

$\displaystyle =\int\limits_{0}^{1}\sum\limits_{i=0}^{\infty}\frac{\beta^{2i}}{2i+1}\;d\beta =\sum\limits_{i=0}^{\infty}\frac{1}{(2i+1)^2} \quad \overset{J(1)=\frac{\pi^2}{8}, J(0)=0}{\implies} \quad \sum\limits_{i=0}^{\infty}\frac{1}{(2i+1)^2}= \frac{\pi^2}{8}$

For full-length proof, read my posting “An Analytic Proof of the Extraordinary Euler Sum” on

https://nuomegamath.wordpress.com/2024/04/02

Many of you may know Dr. Zeilberger, “a champion of using computers and algorithms to perform mathematics quickly and efficiently.” (Wikipedia) You can find more about his work on his website. After completing the proof a few days ago, I reached out to him for a review. He graciously agreed to do so at short notice. Dr. Zeilberger is known for his straightforward style, always telling it like it is.

Dr. Zeilberger, Professor at Rutgers University.

https://sites.math.rutgers.edu/~zeilberg/

I would like to revisit example 3 and solve it using a different approach than Feynman’s. This aligns with Feynman’s fundamental principle of not fooling oneself and emphasizes the importance of viewing problems from entirely new perspectives.

Question: WWFD?

Answer: I see $A = \displaystyle\int\limits_{-\infty}^{0}e^y\; dy= e^y\bigg|_{-\infty}^{0} = 1-0 =1$ and $\displaystyle \int\limits_{0}^{1}|\log(x)|\;dx = A.$ Since for $0 < x \le 1, \log(x) \le 0,$ I have $\displaystyle\int\limits_{0}^{1}-\log(x)\;dx=A$ so $\displaystyle\int_{0}^{1}\log(x)\;dx = -A = -1$

An Analytic Proof of the Extraordinary Euler Sum

April 2, 2024April 17, 2024 / Michael Xue / Leave a comment

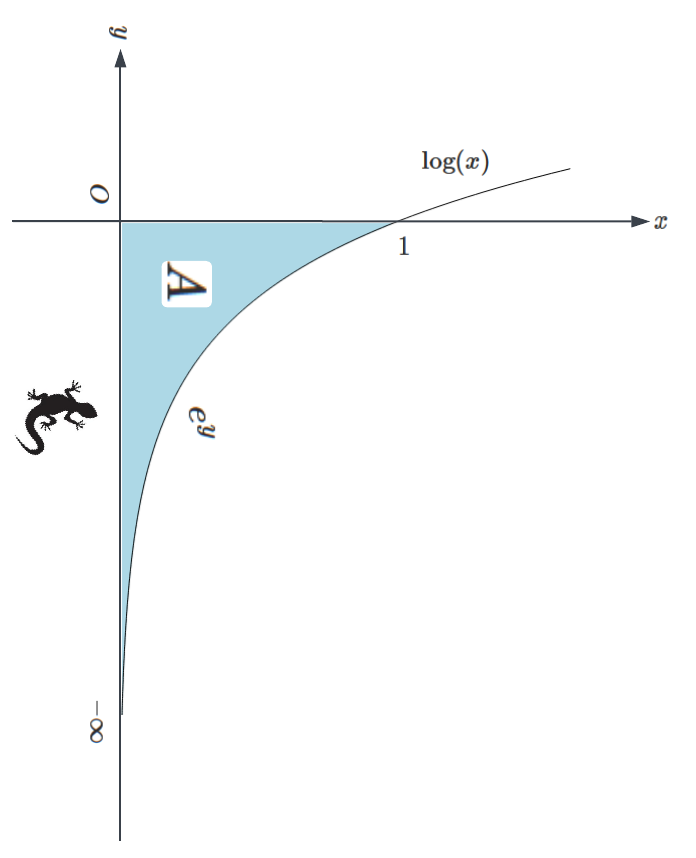
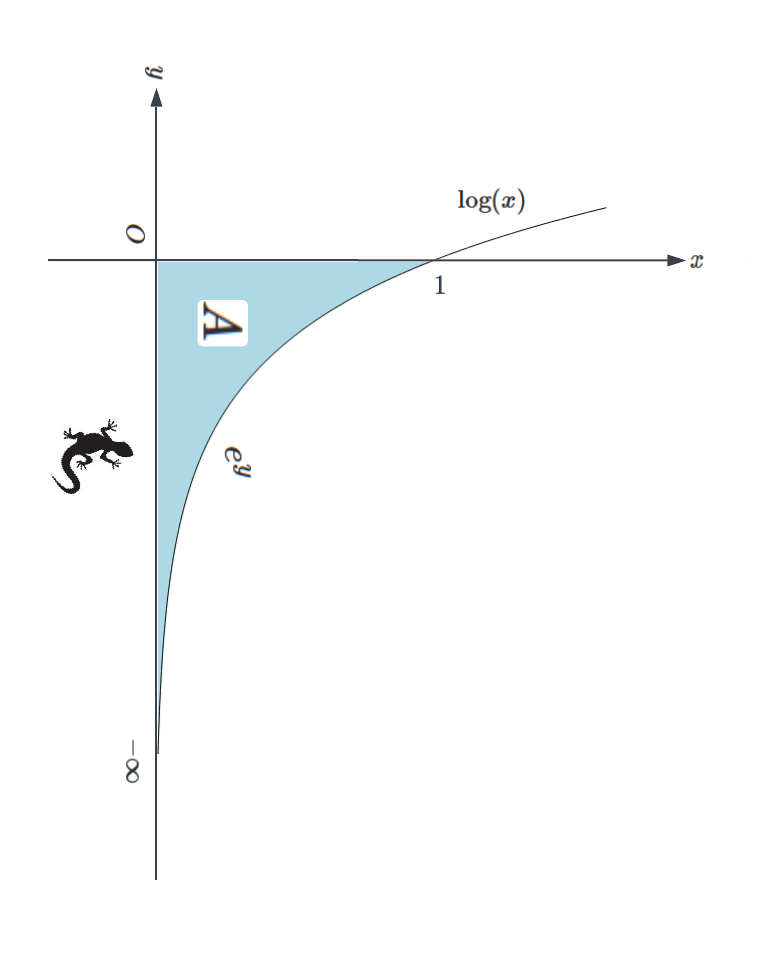
In Deriving the Extraordinary Euler Sum , we derived one of Euler’s most celebrated results:

$\displaystyle 1 + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + ... = \frac{\pi^2}{6}\quad\quad\quad(1)$

Now, we aim to provide a rigorous proof of this statement.

First, we expressed the partial sum of the left-hand side as follows:

$\displaystyle \sum\limits_{i=1}\frac{1}{i^2} = \sum\limits_{i=1}\frac{1}{(2i)^2} + \sum\limits_{i=0}\frac{1}{(2i+1)^2}$

This splits the partial sum into two parts: one involving the squares of even numbers and the other involving the squares of odd numbers. Simplifying the even part gives us:

$\displaystyle \sum\limits_{i=1}\frac{1}{i^2} = \frac{1}{4}\sum\limits_{i=1}\frac{1}{i^2} + \sum\limits_{i=0}\frac{1}{(2i+1)^2}$

Rearranging terms $\displaystyle \sum\limits_{i=1}\frac{1}{i^2}$ on one side, we obtain:

$\displaystyle \frac{3}{4}\sum\limits_{i=1}\frac{1}{i^2}=\sum\limits_{i=0}\frac{1}{(2i+1)^2}$

Since $\displaystyle \sum_{i=1}\frac{1}{i^2}$ converges to $\displaystyle \sum_{i = 1}^{\infty}\frac{1}{i^2}$ (see My Shot at Harmonic Series)

$\displaystyle \implies \sum\limits_{i=0} \frac{1}{(2i+1)^2}$ converges to $\displaystyle \sum\limits_{i=0}^{\infty}\frac{1}{(2i+1)^2} = \frac{3}{4}\sum\limits_{i=1}^{\infty}\frac{1}{i^2},$

to prove (1), it suffices to demonstrate that

$\displaystyle \frac{4}{3}\sum\limits_{i=0}^{\infty}\frac{1}{(2i+1)^2} = \frac{\pi^2}{6}$

or equivalently,

$\displaystyle \sum\limits_{i=0}^{\infty}\frac{1}{(2i+1)^2} = \frac{\pi^2}{8}\quad\quad\quad(2)$

Let $\displaystyle I = \int\limits_{0}^{\infty}\frac{\arctan(x)}{1+x^2}\;dx$ and $J(\beta) = \displaystyle \int\limits_{0}^{\infty}\frac{\arctan(\beta x)}{1+x^2}\;dx,$ we have

$\displaystyle J(1) = I = \frac{1}{2}\arctan^2(x)\bigg|_{0}^{\infty} = \frac{1}{2}\left(\frac{\pi}{2}\right)^2=\frac{\pi^2}{8}\quad\quad\quad(3)$

and

$J(0) = 0\quad\quad\quad(4)$

Differentiating $\displaystyle J(\beta)$ with respect to $\beta:$

$\frac{d}{d\beta}J(\beta) = \displaystyle\frac{d}{d\beta}\int\limits_{0}^{\infty}\frac{\arctan(\beta x)}{1+x^2}\;dx = \int\limits_{0}^{\infty}\frac{\partial}{\partial \beta}\left(\frac{\arctan(\beta x)}{1+x^2}\right)\;dx$

$= \displaystyle \int\limits_{0}^{\infty}\frac{1}{1+x^2}\cdot\frac{x}{\beta^2x^2+1}\;dx$

That is,

$\frac{d}{d\beta}J(\beta) = \displaystyle \int\limits_{0}^{\infty}\frac{x}{(1+x^2)(\beta^2x^2+1)}\;dx$

Integrating with respect to $\beta$ from $0$ to $1:$

$\displaystyle\int\limits_{0}^{1}\frac{d}{d\beta}J(\beta)\;d\beta = \int\limits_{0}^{1}\int\limits_{0}^{\infty}\frac{x}{(1+x^2)(\beta^2 x^2+1)}\;dx\;d\beta$

and expressing the integrand in partial fractions:

yields

$J(1) - J(0) = \displaystyle\int\limits_{0}^{1}\int\limits_{0}^{\infty}\frac{1}{\beta^2-1}\left(\frac{\beta^2x}{\beta^2x^2+1} - \frac{x}{x^2+1}\right)\;dx\;d\beta$

$= \displaystyle\int\limits_{0}^{1}\int\limits_{0}^{\infty}\frac{1}{\beta^2-1}\cdot\frac{1}{2}\cdot\left(\frac{2\beta^2x}{\beta^2x^2+1} - \frac{2x}{x^2+1}\right)\;dx\;d\beta$

$= \displaystyle\int\limits_{0}^{1}\frac{1}{2(\beta^2-1)}\int\limits_{0}^{\infty}\left(\frac{2\beta^2x}{\beta^2x^2+1} - \frac{2x}{x^2+1}\right)\;dx\;d\beta$

$= \displaystyle\int\limits_{0}^{1}\frac{1}{2(\beta^2-1)}\log\left(\frac{\beta^2 x^2+1}{x^2+1}\right)\bigg|_{0}^{\infty}\;d\beta$

$= \displaystyle\int\limits_{0}^{1}\frac{1}{2(\beta^2-1)}\lim\limits_{x \rightarrow \infty}\log\left(\frac{\beta^2 x^2+1}{x^2+1}\right)\;d\beta = \displaystyle\int\limits_{0}^{1}\frac{1}{2(\beta^2-1)}\lim\limits_{x \rightarrow \infty}\log\left(\frac{\beta^2 + \frac{1}{x^2}}{1+\frac{1}{x^2}}\right)\;d\beta$

$= \displaystyle\int\limits_{0}^{1}\frac{1}{2(\beta^2-1)}\log(\beta^2)\;d\beta=\boxed{\int\limits_{0}^{1}\frac{\log(\beta)}{\beta^2-1}\;d\beta=\displaystyle\int\limits_{0}^{1}\sum\limits_{i=0}^{\infty}\frac{\beta^{2i}}{2i+1}\;d\beta \quad\quad(\star)}$

$= \displaystyle\sum\limits_{i=0}^{\infty}\int\limits_{0}^{1}\frac{\beta^{2i}}{2i+1}\;d\beta= \displaystyle\sum\limits_{i=0}^{\infty}\left(\frac{1}{2i+1}\underline{\int\limits_{0}^{1}\beta^{2i}\;d\beta}\right)=\sum\limits_{i=0}^{\infty}\frac{1}{2i+1}\cdot\underline{\frac{\beta^{2i+1}}{2i+1}\bigg|_{0}^{1}}$

$= \displaystyle\sum\limits_{i=0}^{\infty}\frac{1}{(2i+1)^2}$

i.e.,

$J(1)-J(0) = \displaystyle\sum\limits_{i=0}^{\infty}\frac{1}{(2i+1)^2}.$

By (3) and (4),

$\displaystyle\frac{\pi^2}{8}-0 =\sum\limits_{i=0}^{\infty}\frac{1}{(2i+1)^2}$

$\displaystyle\sum\limits_{i=0}^{\infty}\frac{1}{(2i+1)^2} = \frac{\pi^2}{8}$

which is (2)

Prove $\boxed{\int\limits_{0}^{1}\frac{\log(\beta)}{\beta^2-1}\;d\beta=\displaystyle\int\limits_{0}^{1}\sum\limits_{i=0}^{\infty}\frac{\beta^{2i}}{2i+1}\;d\beta \quad\quad(\star)}$

Since

$\displaystyle\frac{d}{d\beta}v = \frac{1}{\beta^2-1} = \frac{1}{\beta-1}-\frac{1}{\beta+1}$

means

$v = \displaystyle \frac{1}{2}\int\frac{1}{\beta-1}-\frac{1}{\beta+1}\;d\beta = \frac{1}{2}\log\left(\frac{|\beta-1|}{|\beta+1|}\right) \overset{\beta \le 1}{=}\frac{1}{2}\log\left(\frac{1-\beta}{\beta+1}\right),$

we have

$\displaystyle\int\limits_{0}^{1}\frac{\log(\beta)}{\beta^2-1}\;d\beta = \int\limits_{0}^{1}\log(\beta)\cdot\frac{d}{d\beta}\left(\frac{1}{2}\log\left(\frac{1-\beta}{1+\beta}\right)\right)\;d\beta$

$= \displaystyle\log(\beta)\cdot\frac{1}{2}\log\left(\frac{1-\beta}{1+\beta}\right)\bigg|_{0}^{1} - \int\limits_{0}^{1}\frac{1}{\beta}\cdot\frac{1}{2}\log\left(\frac{1-\beta}{1+\beta}\right)\;d\beta$

$= \displaystyle\frac{1}{2}\cdot\underline{\log\left(\beta\right)\log\left(\frac{1-\beta}{1+\beta}\right)\bigg|_{0}^{1}} - \int\limits_{0}^{1}\frac{1}{\beta}\cdot\frac{1}{2}\log\left(\frac{1-\beta}{1+\beta}\right)\;d\beta$

$\boxed{\log\left(\beta\right)\log\left(\frac{1-\beta}{1+\beta}\right)\bigg|_{0}^{1}=0\quad\quad\quad(\star\star)}$

$= \displaystyle\int\limits_{0}^{1}\frac{1}{\beta}\cdot\frac{1}{2}\cdot\log\left(\frac{1+\beta}{1-\beta}\right)\;d\beta$

Expand $\log(\frac{1+\beta}{1-\beta})$ into its Maclaurin series:

$= \displaystyle \int\limits_{0}^{1}\frac{1}{\beta}\cdot\frac{1}{2}\cdot2\sum\limits_{i=0}^{\infty}\frac{\beta^{2i+1}}{2i+1}\;d\beta = \int\limits_{0}^{1}\sum\limits_{i=0}^{\infty}\frac{\beta^{2i}}{2i+1}\;d\beta$

Prove $\boxed{\log\left(\beta\right)\log\left(\frac{1-\beta}{1+\beta}\right)\bigg|_{0}^{1}=0\quad\quad\quad(\star\star)}$

For $\displaystyle k \in \mathbb{R}, \log(x)\log(1+kx) = \log(x)\cdot x \cdot \frac{1}{x}\cdot\log(1+kx) = \log(x)x \cdot \frac{\log(1+kx)}{x}$

We have

$\displaystyle\lim\limits_{x \rightarrow 0}\log(x)x = \lim\limits_{x \rightarrow 0} \frac{\log(x)}{\frac{1}{x}}=\lim\limits_{x \rightarrow 0} \frac{\frac{1}{x}}{-\frac{1}{x^2}} = \lim\limits_{x \rightarrow 0}-x = 0$

$\displaystyle \lim\limits_{x \rightarrow 0}\frac{\log(1+kx)}{x} = \lim\limits_{x \rightarrow 0}\frac{\frac{k}{1+kx}}{1} = k.$

As a result,

$\displaystyle \lim\limits_{x \rightarrow 0} \log(x)\log(1+kx) = \lim\limits_{x \rightarrow 0} \log(x)x \cdot \lim\limits_{x \rightarrow 0} \frac{\log(1+kx)}{x}=0\cdot k = 0.$ i.e.,

$\displaystyle \lim\limits_{x \rightarrow 0} \log(x)\log(1+kx) = 0, \quad k \in \mathbb{R}\quad\quad\quad(\star\star-1)$

Moreover,

$\displaystyle \lim\limits_{\beta \rightarrow 1}(\log(\beta)\cdot\log(1-\beta)-\log(\beta)\log(1+\beta))$

$\displaystyle= \lim\limits_{\beta \rightarrow 1}\log(\beta)\cdot\log(1-\beta)-\underbrace{\lim\limits_{\beta \rightarrow 1}\log(\beta)\cdot\log(1+\beta)}_{0}$

Let $\displaystyle x = 1-\beta \implies \beta=1-x$ and $\beta \rightarrow 1 \implies x \rightarrow 0$

$\displaystyle = \lim\limits_{x \rightarrow 0}\log(x)\log(1-x)$

$\displaystyle = \lim\limits_{x \rightarrow 0}\log(x)\log(1+(-1) x) \overset{(\star\star-1)}{=} 0$

gives

$\displaystyle \lim\limits_{\beta \rightarrow 1}(\log(\beta)\log(1-\beta)-\log(\beta)\log(1+\beta))=0.\quad\quad\quad(\star\star-2)$

It follows that

$\displaystyle \log(\beta)\log(\frac{1-\beta}{1+\beta})\bigg|_{0}^{1}$

$\displaystyle = \lim\limits_{\beta \rightarrow 1}\log(\beta)(\log(1-\beta) - \log(1+\beta)) - \lim\limits_{\beta \rightarrow 0}\log(\beta)(\log(1-\beta) - \log(1+\beta))$

$\displaystyle \overset{(\star\star-2)}{=} 0 -\lim\limits_{\beta \rightarrow 0}\log(\beta)\log(1+(-1)\cdot\beta) + \lim\limits_{\beta \rightarrow 0} \log(\beta)\log(1+1\cdot\beta)\overset{(\star\star-1)}{=} 0$

WWFD ?

March 25, 2024March 30, 2024 / Michael Xue / Leave a comment

$\displaystyle \int\limits_{0}^{1}\log(x)\;dx = ?$

For $\beta \ge 0, \displaystyle\int\limits_{0}^{1} x^\beta\; dx= \frac{x^{\beta+1}}{\beta+1}\bigg|_{0}^{1}=\frac{1}{\beta+1}$

$\implies \displaystyle\frac{d}{d\beta}\int\limits_{0}^{1} x^\beta\; dx= \frac{d}{d\beta}\left(\frac{1}{\beta+1}\right)$

$\implies \displaystyle\int\limits_{0}^{1}\frac{\partial}{\partial \beta}x^\beta\;dx = \frac{-1}{(\beta+1)^2}$

$\implies \displaystyle\int\limits_{0}^{1}x^\beta\log(x)\;dx = \frac{-1}{(\beta+1)^2}$

Let $\beta = 0$

$\implies \displaystyle\int\limits_{0}^{1}x^0\log(x)\;dx = \frac{-1}{0+1}$

$\implies \displaystyle\int\limits_{0}^{1}\log(x)\;dx = -1.$

I see $A = \displaystyle\int\limits_{-\infty}^{0}e^y\; dy= e^y\bigg|_{-\infty}^{0} = 1-0 =1$ and $\displaystyle \int\limits_{0}^{1}|\log(x)|\;dx = A.$ Since for $0 < x \le 1, \log(x) \le 0,$ I have $\displaystyle\int\limits_{0}^{1}-\log(x)\;dx=A$ so $\displaystyle\int_{0}^{1}\log(x)\;dx = -A = -1$ .

A Gem from Charles-Ange Laisant

March 22, 2024March 25, 2024 / Michael Xue / Leave a comment

In a 1905 article, Charles-Ange Laisant, a French politician and mathematician, introduced the following theorem:

Given a function $f$ with inverse $f^{-1}$ , then

$\displaystyle \boxed{(y=f(x) \iff x = f^{-1}(y), F'(x) = f(x)) \implies \int f^{-1}(y)\;dy = y f^{-1}(y) - F(x) + C \quad\quad\quad(1)}$

where $C$ is an arbitrary real constant.

It can also be stated equivalently as:

Given a function $f$ with inverse $f^{-1},$ then

$\displaystyle \boxed{(y=f(x) \iff x=f^{-1}(y), F'(y)=f^{-1}(y)) \implies \int f(x)\;dx = x f(x)-F(y) +C \quad\quad\quad(2)}$

where $C$ is an arbitrary real constant.

Moreover, this theorem gives

$\displaystyle \boxed{(y=f(x) \iff x = f^{-1}(y), F'(x) = f(x)) \implies \int\limits_{b}^{a} f^{-1}(y)dy = bf^{-1}(b)-af^{-1}(a) - (F(f^{-1}(b))-F(f^{-1}(a)))\quad\quad\quad(3)}$

and

$\displaystyle \boxed{(y=f(x) \iff x = f^{-1}(y), F'(y) = f^{-1}(y)) \implies \int\limits_{a}^{b}f(x)\;dx=bf(b)-af(a) - (F(f(b))-F(f(a))\quad\quad\quad(4)}$

Frequently, obtaining an antiderivative for $f^{-1}$ is relatively easier than finding one for $f$ . In such instances, substituting the integrals of $f$ with integrals involving $f^{-1}$ can be advantageous.

For example, let $f=\arcsin \implies f^{-1} = \sin,$ we have

$\displaystyle F'(y) = f^{-1}(y) = \sin(y) \implies F(y) = \int \sin(y)\; dy = -\cos(y) + C_1.$

As a result,

$\displaystyle \int \arcsin(x)\;dx \overset{(2)}{=} x \arcsin(x) - F(y)$

$= x \arcsin(x) - (-\cos(y)+C_1)$

$y=f(x)=\arcsin(x) \implies \left(-\frac{\pi}{2} \le y \le \frac{\pi}{2}, x = \sin(y)\right)$

$\implies \cos(y) = +\sqrt{1-\sin(y)} = \sqrt{1-x^2}.$

$= x \arcsin(x) + \sqrt{1-x^2} + C, \quad C=-C_1.$

That is,

$\displaystyle\int \arcsin(x)\;dx = x \arcsin(x) + \sqrt{1-x^2}+C.$

Another illuminating example is as follows:

$\displaystyle \int\limits_{0}^{1}\log(x)\;dx$

$= \displaystyle \lim\limits_{a \rightarrow 0^+}\int\limits_{a}^{1}\log(x)\;dx$

$f = \log \implies f^{-1} = \exp.$

$\overset{(4)}{=} \displaystyle\lim\limits_{a \rightarrow 0^+}\left(x\log(x)\bigg|_{a}^{1}-(e^{\log(1)} - e^{\log(a))}\right)$

$= \displaystyle\lim\limits_{a \rightarrow 0^+}\left(1\cdot\log(1)-a\cdot\log(a)-(1-a)\right)$

$= \lim\limits_{a \rightarrow 0^+}(-a\cdot\log(a) - (1-a)).$

Since $\boxed{\lim\limits_{a \rightarrow 0^+} a\cdot\log(a)=0}, \; \lim\limits_{a \rightarrow 0^+} 1-a = 1,$ we have

$\displaystyle \int\limits_{0}^{1}\log(x)\;dx= -1.$

Prove $\displaystyle \boxed{(y=f(x) \iff x = f^{-1}(y), F'(x) = f(x)) \implies \int f^{-1}(y)\;dy = y f^{-1}(y) - F(x) + C \quad\quad\quad(1)}$

$\frac{d}{dy} (yf^{-1}(y)-F(y) + C)$

$= \frac{d}{dy}yf^{-1}(y) + y\frac{d}{dy}f^{-1}(y) -\frac{d}{dy}F(x) + \frac{d}{dy}C$

$\overset{y=f(x)}{=} f^{-1}(y) + f(x) \frac{d}{dy}f^{-1}(y) -\frac{d}{dx}F(x)\frac{d}{dy}x + 0$

$\overset{F'(x)=f(x), x=f^{-1}(y)}{=} f^{-1}(y) +f(x)\frac{d}{dy}f^{-1}(y) -f(x)\frac{d}{dy}f^{-1}(y)$

$= f^{-1}(y)$

$\implies yf^{-1}(y) - F(x) + C$ is an antiderivative of $f^{-1}(y).$

Therefore, $\displaystyle \int f^{-1}(y)\;dy = y f^{-1}(y) - F(x)) + C.$

Prove $\displaystyle \boxed{(y=f(x) \iff x = f^{-1}(y), F'(y) = f^{-1}(y)) \implies\int\limits_{a}^{b}f(x)\;dx=bf(b)-af(a) - (F(f(b))-F(f(a))\quad\quad\quad(4)}$

By (2),

$\displaystyle\int\limits_{a}^{b}f(x)\;dx \overset{y=f(x)}{=} xf(x)-F(f(x))+C\bigg|_{a}^{b}$

$=bf(b)-F(f(b)) - (af(a)-F(f(a)))$

$= bf(b)-af(a) - (\underbrace{F(f(b))-F(f(a))}_{\displaystyle \int_{f(b)}^{f(a)}f^{-1}(x)\;dx})$

Prove $\boxed{\lim\limits_{a \rightarrow 0^+} a\cdot\log(a)=0}:$

$\lim\limits_{a \rightarrow 0^+} a\cdot\log(a)=\lim\limits_{a \rightarrow 0^+} \frac{\log(a)}{\frac{1}{a}}$

$\overset{\lim\limits_{a \rightarrow 0^+}\log(a) = -\infty, \lim\limits_{a \rightarrow 0^+}\frac{1}{a} = \infty}{=} \lim\limits_{a \rightarrow 0^+} \frac{\frac{d}{da}(\log(a))}{\frac{d}{da}(\frac{1}{a})}= \lim\limits_{a \rightarrow 0^+} \frac{\frac{1}{a}}{-\frac{1}{a^2}}= \lim\limits_{a \rightarrow 0^+} -a= 0.$

Exercise-1 Prove (2)

Exercise-2 Prove (3)

Exercise-3 What is $\displaystyle \int \arctan(x)\;dx ?$

(Hint: $\displaystyle \int \tan(x)\;dx = \log(|\sec(x)|), 1+\tan^2(x)=\sec^2(x)$ )

Exercise-4 Explain $\lim\limits_{a \rightarrow 0^+}\log(a) = -\infty$ and $\lim\limits_{a \rightarrow 0^+}\frac{1}{a} = \infty.$

Exercise-5 Show that (2) can be written as

$\displaystyle \int f(x)\;dx = xf(x)-\int f^{-1}(y)\;dy + C.$

And, prove

$\displaystyle \int f^p(x)\;dx = xf^p(x)-p\int y^{p-1} f^{-1}(y)\;dy + C, \quad p\in \mathbb{R}.$

Exercise-6 Derive (1) (Hint: The foundation of a technique for evaluating definite integrals and Integration by Parts Done Right)

A Tango of Limits and Infinity

March 15, 2024March 15, 2024 / Michael Xue / Leave a comment

Prove:

$\lim\limits_{x \rightarrow \infty} \arctan(x) = \frac{\pi}{2}$

For any positive number $\epsilon$ , let $x^* = \tan(\frac{\pi}{2}-\epsilon).$

Since $\arctan$ is a monotonic increasing function: $(\arctan(x))' = \frac{1}{1+x^2} > 0,$

we have

$\forall x > x^*, \arctan(x) > \arctan(x^*) = \arctan(\underbrace{\tan(\frac{\pi}{2}-\epsilon)}_{x^*}) = \frac{\pi}{2}-\epsilon.$

That is,

$\arctan(x) > \frac{\pi}{2}-\epsilon$

$-\epsilon + \frac{\pi}{2} < \arctan(x).\quad\quad\quad(1)$

By the definition of $\arctan(x)$ :

$\arctan \overset{\Delta}{=}\{(x, y) | \tan(y) = x, x \in \mathbb{R}, -\frac{\pi}{2} < y < \frac{\pi}{2}\},$

we also have

$\arctan(x) < \frac{\pi}{2} < \frac{\pi}{2} + \epsilon.\quad\quad\quad(2)$

Combining (1) and (2) gives

$-\epsilon + \frac{\pi}{2} < \arctan(x) < \epsilon + \frac{\pi}{2} \implies |\arctan(x)-\frac{\pi}{2}| < \epsilon.$

This implies that

$\forall \epsilon > 0, \exists x^* \ni x>x^* , |\arctan(x)-\frac{\pi}{2}| < \epsilon.$

In other words,

$\lim\limits_{x \rightarrow \infty} \arctan(x) = \frac{\pi}{2}.$

A Melody on Pi Day

March 14, 2024March 15, 2024 / Michael Xue / Leave a comment

Evaluate $\displaystyle \int\limits_{-\infty}^{\infty} \frac{\sin(x)}{x}\;dx$

This integral is known as the Dirichlet Integral, named in honor of the esteemed German mathematician Peter Dirichlet. Due to the absence of an elementary antiderivative for the integrand, its evaluation by applying the Newton-Leibniz rule renders an impasse. However, the Feynman’s integral technique offers a solution.

The even nature of the function $\frac{\sin(x)}{x}$ implies that

$\displaystyle\int\limits_{-\infty}^{\infty}\frac{\sin(x)}{x}\;dx = 2 \int\limits_{0}^{\infty}\frac{\sin(x)}{x}\;dx.\quad\quad\quad(*)$

Let’s consider

$I = \displaystyle\int\limits_{0}^{\infty} \frac{\sin(x)}{x}\;dx\quad\quad\quad(**)$

and define

$J(\beta) = \displaystyle\int\limits_{0}^{\infty} \frac{\sin(x)}{x}e^{-\beta x}\;dx ,\quad\beta\ge 0.\quad\quad\quad(***)$

We can differentiate $J(\beta)$ with respect to $\beta:$

$\frac{dJ(\beta)}{d\beta} = \displaystyle\int\limits_{0}^{\infty}\frac{\partial}{\partial\beta} \left(\frac{\sin(x)}{x}e^{-\beta x}\right)\;dx= \displaystyle \int\limits_{0}^{\infty}\frac{\sin(x)}{x}\cdot(-x) e^{-\beta x}\;dx= \boxed{\displaystyle\int\limits_{0}^{\infty}-\sin(x)e^{-\beta x}\;dx=\frac{-1}{1+\beta^2}}.$

Hence, we find

$\frac{dJ(\beta)}{d\beta} = \frac{-1}{1+\beta^2}.$

Integrating with respect to $\beta$ from $0$ to $\infty :$

$\displaystyle\int\limits_{0}^{\infty} \frac{dJ(\beta)}{d\beta}\;d\beta = \int\limits_{0}^{\infty}\frac{-1}{1+\beta^2}\;d\beta$

$= -\arctan(\beta)\bigg|_{0}^{\infty}=\left(\lim\limits_{\beta\rightarrow \infty}-\arctan(\beta)\right)-\left(-\arctan(0)\right)=-\frac{\pi}{2}$

gives

$J(\infty)-J(0) = -\frac{\pi}{2}.$

Since

$J(0) = \displaystyle\int\limits_{0}^{\infty}\frac{\sin(x)}{x}e^{-0\cdot x}\;dx = \int\limits_{0}^{\infty}\frac{\sin(x)}{x}\;dx \overset{(**)}{=}I$

and

$\boxed{J(\infty) = 0}$ ,

we arrive at

$0 - I = -\frac{\pi}{2} \implies I = \frac{\pi}{2}\overset{(**)}{\implies} \displaystyle \int\limits_{0}^{\infty} \frac{\sin(x)}{x}\;dx=\frac{\pi}{2}.$

It follows that by (*):

$\displaystyle\int\limits_{-\infty}^{\infty}\frac{\sin(x)}{x}\;dx = \pi.$

Show that $\boxed{J(\infty) = 0}:$

From the inequality

$\forall x>0, \frac{\sin(x)}{x}e^{-\beta x} > 0$

and

$\forall x > 0, \frac{\sin(x)}{x} < 1$

(see (3) in A Proof without Calculus),

we deduce that

$\displaystyle 0 < \int\limits_{0}^{\infty}\frac{\sin(x)}{x}e^{-\beta x}\;dx < \int\limits_{0}^{\infty}e^{-\beta x}\; dx = \frac{-e^{-\beta x}}{\beta} \bigg|_{0}^{\infty} = (\lim\limits_{x \rightarrow \infty} \frac{-e^{-\beta x}}{\beta})-\frac{-e^{\beta\cdot 0}}{\beta}= \frac{1}{\beta}.$

That is,

$\displaystyle 0 < \int\limits_{0}^{\infty}\frac{\sin(x)}{x}e^{-\beta x}\;dx < \frac{1}{\beta}.$

By the Sandwich Theorem for Functions 2,

$\lim\limits_{\beta \rightarrow \infty}\frac{1}{\beta } = 0 \implies \displaystyle\lim\limits_{\beta \rightarrow }\int\limits_{0}^{\infty}\frac{\sin(x)}{x}e^{-\beta x}\;dx =0.\quad\quad\quad(\star)$

Consequently,

$J(\infty) = \lim\limits_{\beta \rightarrow \infty} J(\beta) \overset{(***)}{=}\displaystyle\lim\limits_{\beta \rightarrow \infty}\int\limits_{0}^{\infty}\frac{\sin(x)}{x}e^{-\beta x}\;dx\overset{(\star)}{\implies} J(\infty) = 0.$

Show that $\displaystyle \boxed{\int\limits_{0}^{\infty} -\sin(x)e^{-\beta x}\;dx=\frac{-1}{1+\beta^2}}:$

$\displaystyle \int\limits_{0}^{\infty} -\sin(x)e^{-\beta x}\;dx$

$= \displaystyle\int\limits_{0}^{\infty} (\cos(x))'e^{-\beta x}\;dx$

$= \displaystyle \cos(x)e^{-\beta x}\bigg|_{0}^{\infty} - \int\limits_{0}^{\infty}e^{-\beta x}\cdot -\beta \cdot \cos(x)\; dx$

$= \displaystyle 0 - 1 + \beta\int\limits_{0}^{\infty} e^{-\beta x}\cos(x)\;dx$

$= \displaystyle -1 + \beta\left(\sin(x)e^{-\beta x}\bigg|_{0}^{\infty}-\beta\int\limits_{0}^{\infty}-\sin(x)e^{-\beta x}\; dx\right)$

$=\displaystyle -1 -\beta^2\int\limits_{0}^{\infty}-\sin(x)e^{-\beta x}\; dx.$

That is,

$\displaystyle\underline{\int\limits_{0}^{\infty}-\sin(x)e^{-\beta x} \;dx} = -1 - \beta^2\underline{\int\limits_{0}^{\infty}-\sin(x)e^{-\beta x} \;dx}.$

Therefore,

$\displaystyle (1+\beta^2)\int\limits_{0}^{\infty}-\sin(x)e^{-\beta x}\;dx = -1 \implies \int\limits_{0}^{\infty}-\sin(x)e^{-\beta x}\;dx =\frac{-1}{1+\beta^2}.$

Exercise-1 Evaluate $\displaystyle \int\limits_{0}^{\infty} -\sin(x)e^{-\beta x}\;dx$ by the schematic method (hint: Schematic Integration by Parts)

Sandwich Theorem for Functions 2

March 12, 2024April 5, 2024 / Michael Xue / Leave a comment

For given functions $f(x), g(x),$ and $h(x),$

$\left(\forall x : f(x) \le g(x) \le h(x), \lim\limits_{x \rightarrow \infty} f(x) = \lim\limits_{x \rightarrow \infty} h(x)=L\right) \implies \lim\limits_{x \rightarrow \infty} g(x) = L.$