The Russian multiplication method is an alternative algorithm for multiplying two numbers. It states:
[1] Place two numbers to be multiplied at the head of two columns.
[2] The number in the first column is continuously divided by 2, ignoring reminders, until the number 1 is reached. The number in the second column is continuously doubled, until it reaches the last row of the first column.
[3] Now cross out all numbers in the second column that are in line with even numbers from the first column.
[4] The product is given by adding the remaining numbers in the second column.
For example, to multiply 158 and 39,
The result is 78 + 156 + 312 + 624 + 4992 = 6162.
To understand this algorithm, we let

where  ; all other
; all other 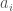 s and
s and 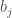 s are either
s are either 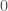 or
or 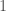 .
.
As a result,




After depicting 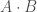 by the Russian multiplication method in Fig. 1:
by the Russian multiplication method in Fig. 1:

Fig. 1
we see for a given 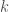 , if
, if  is an even number, then
is an even number, then 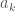 must be
must be  Consequently,
Consequently,

It means on any given row, if the first column contains an even number, the second column will take no part in summation 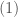 . This is equivalent to “cross out all numbers in the second column that are in line with even numbers from the first column”. Adding the remaining numbers in the second column then gives
. This is equivalent to “cross out all numbers in the second column that are in line with even numbers from the first column”. Adding the remaining numbers in the second column then gives 
See also “Schematic Integration by Parts“.
This, therefore, is mathematics: she gives life to her own discoveries; she awakens the mind and purifies the intellect; she brings light to our intrinsic ideas; she abolishes the oblivion and ignorance which are ours by birth.
– Proclus , a Greek commentator of the 5th centry

. That is,
.
.
,
,
,
.
.
.
:






