We will study a simple chemical reaction described by

where two molecules of 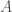 are combined reversibly to form
are combined reversibly to form  and,
and, 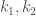 are the reaction rates.
are the reaction rates.
If  is the concentration of
is the concentration of 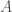 ,
, 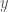 of
of  , then according to the Law of Mass Action,
, then according to the Law of Mass Action,

or equivalently,
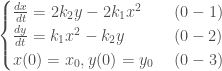
We seek first the equilibrium points that represent the steady state of the system. They are the constant solutions where  and
and  , simultaneously.
, simultaneously.
From  and
and 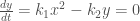 , it is apparent that
, it is apparent that

is an equilibrium point.
To find the value of 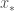 , we solve for
, we solve for 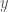 from (0-1),
from (0-1),
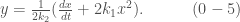
Substitute it in (0-2),
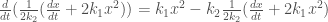
 ,
,
i.e.,

This is a 2nd order nonlinear differential equaion. Since it has no direct dependence on  , we can reduce its order by appropriate substitution of its first order derivative.
, we can reduce its order by appropriate substitution of its first order derivative.
Let
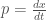 ,
,
we have
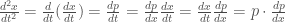
so that (0-6) is reduced to

a 1st order differential eqution. It follows that either  or
or  .
.
The second case gives
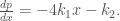
Integrate it with respect to  ,
,
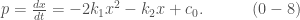
Hence, the equilibrium points of (0-1) and (0-2) can be obtained by solving a quadratic equation
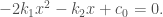
Notice in order to have  as a solution,
as a solution, 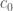 must be non-negative .
must be non-negative .
Fig. 1
The valid solution is

Fig. 2
By (0-4),

and so, the equilibrium point is
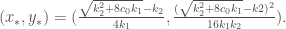
Next, we turn our attentions to the phase-plan trajectories that describe the paths traced out by the 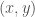 pairs over the course of time, depending on the initial values.
pairs over the course of time, depending on the initial values.
For  . Dividing (0-2) by (0-1) yields
. Dividing (0-2) by (0-1) yields

i.e.,

Integrating it with respect to  ,
,

By (0-3),

Therefore,

Moreover, by (0-5)

As a result,
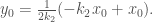
Substitute 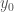 in (1-1), we have
in (1-1), we have

This is the trajectory of the system. Clearly, all trajectories are monotonically decreaseing lines.
At last, let us examine how the system behaves in the long run.
If  then
then  (see Fig. 2) and
(see Fig. 2) and  will increase. As a result,
will increase. As a result, 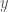 will decrease. Similarly, if
will decrease. Similarly, if  ensures that
ensures that  will decrease. Consequently,
will decrease. Consequently, 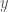 will increase.
will increase.
Fig. 3 Trajectories and Equilibriums
It is evident that as time  advances,
advances, 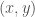 on the trajectory approaches the equilibrium point
on the trajectory approaches the equilibrium point 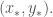
A phase portrait of the system is illustrated in Fig. 4.
Fig. 4
It shows that the system is asymptotically stable.

quantitatively.
, using a popular symbolic differential equation solver such as ‘ode2’. Then compute
as
, followed by
.


directly from polynormial equation
if
. For example, when
,
has three roots (see Fig. 3).

of equilibrium
(see Exercise-1).
from















