
The fantastic fire bird fractal above is produced by Omega CAS Explorer:
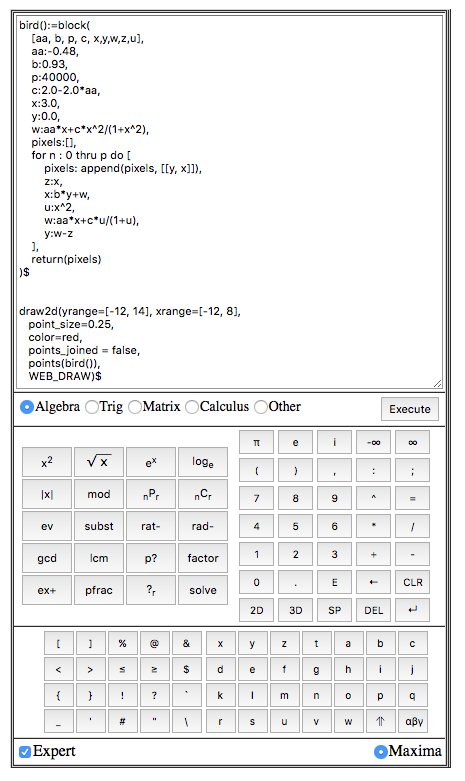
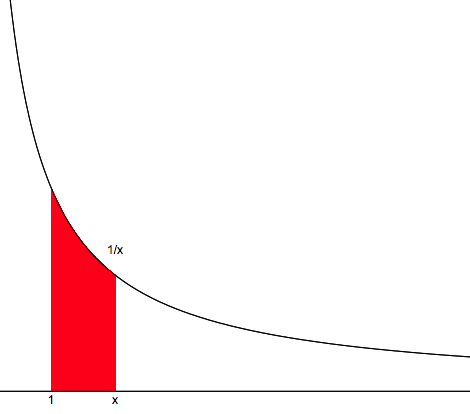
Fig. 1
In my previous blog “A Case of Pre-FTC Definite Integration“, we obtained result
without the Fundamental Theorem of Calculus.
Let’s now consider the case of where
. Namely,
, the area under the curve from 1 to
.
Closed form result (1) is not applicable since .
Attempt of finding the limit of a sum quickly bites the dust too due to the fact that .
However, let
We see immediately that , i.e.,
Other properties of function can be extracted from (2), as shown below:
By definition,
,
and
.
Therefore,
Let , we have
,
i.e.,
By (3-2),
,
i.e.,
Let ,
When ,
.
Assume when where
, we have
Hence,
Moreover, where
,
As result,
With (3-4), (3-5) and (3-6), we conclude that
We will leave this post with the following observation:
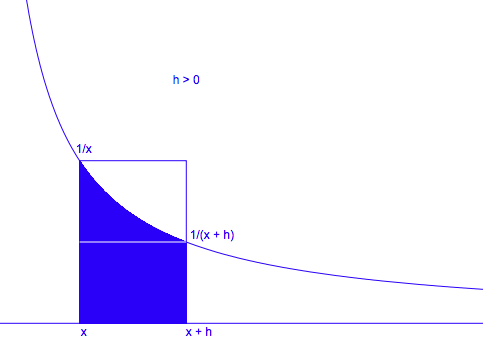
Fig. 2
This is not difficult to see. , if
, then from Fig. 2, we have
area in blue .
The fact that
area in blue
means
,
or,
,
Since ,
from which (4) is obtained (see “Sandwich Theorem for Functions“).
When , area in blue is
.
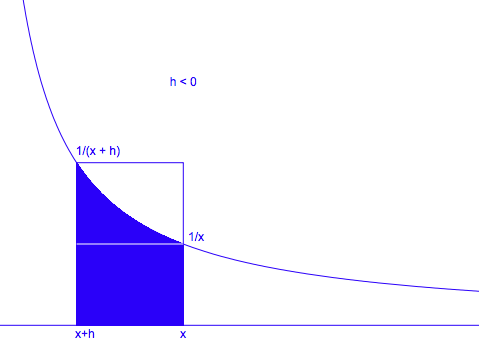
Fig. 3
From Fig. 3 we see that
.
Hence
,
from which (4) is obtained again.