Let us turn our attention to the numerical calculation of logarithm, introduced in my previous post “Introducing Lady L“.
An example of naively compute  , based solely on its definition is shown in Fig. 1.
, based solely on its definition is shown in Fig. 1.
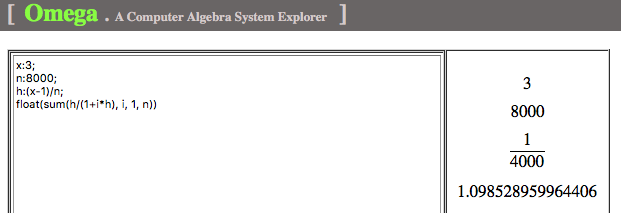
Fig. 1
However, a more explicit expression is better suited for this purpose.
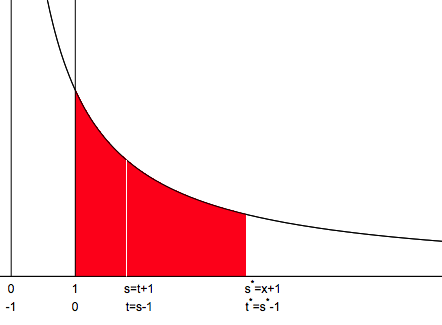
Fig. 2
From Fig.2, geometrical Interpretation of  as the shaded area reveals that
as the shaded area reveals that


 ,
,
i.e.,

Inserting into (1) the well known result
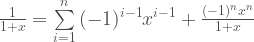 ,
,
we obtain



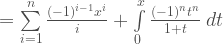 .
.
Let
 ,
,
we have
 .
.
If  ,
,

otherwise (
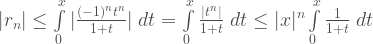 .
.
Therefore, either

or
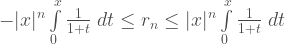 .
.
Since 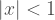 ,
,

and

We conclude that
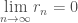 .
.
As a consequence,



 ,
,
i.e.,
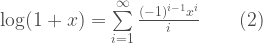
(2) offers a means for finding the numerical values of logarithm. However, its range is limited to the value of  between 0 and 2, since
between 0 and 2, since 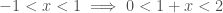 .
.
To overcome this limitation, we proceed as follows:
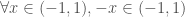 . By (2),
. By (2),

i.e.,
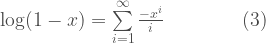
Subtracting (3) from (2) and using the fact that  , we have
, we have


 .
.
i.e.,

Solving equation
 where
where  ,
,
we find
 .
.
Since this solution can be expressed as
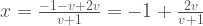
or
 .
.
It shows that for any  ,
,  . Therefore, (4) can be used to obtain the logarithm of any positive number. For example, to obtain
. Therefore, (4) can be used to obtain the logarithm of any positive number. For example, to obtain  , we solve
, we solve  first and then compute a partial sum of (4) with sufficient large number of terms (see Fig. 3)
first and then compute a partial sum of (4) with sufficient large number of terms (see Fig. 3)
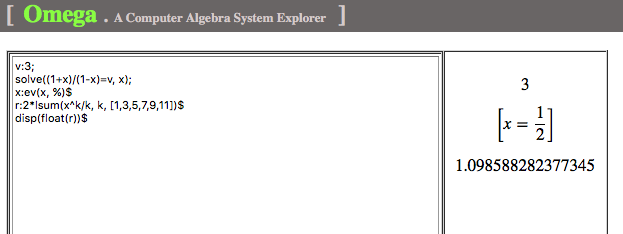
Fig. 3

by
with b = 0.9998, the result is shown in Fig. 2.