
For
Let

I see and
Since for
I have
so
.
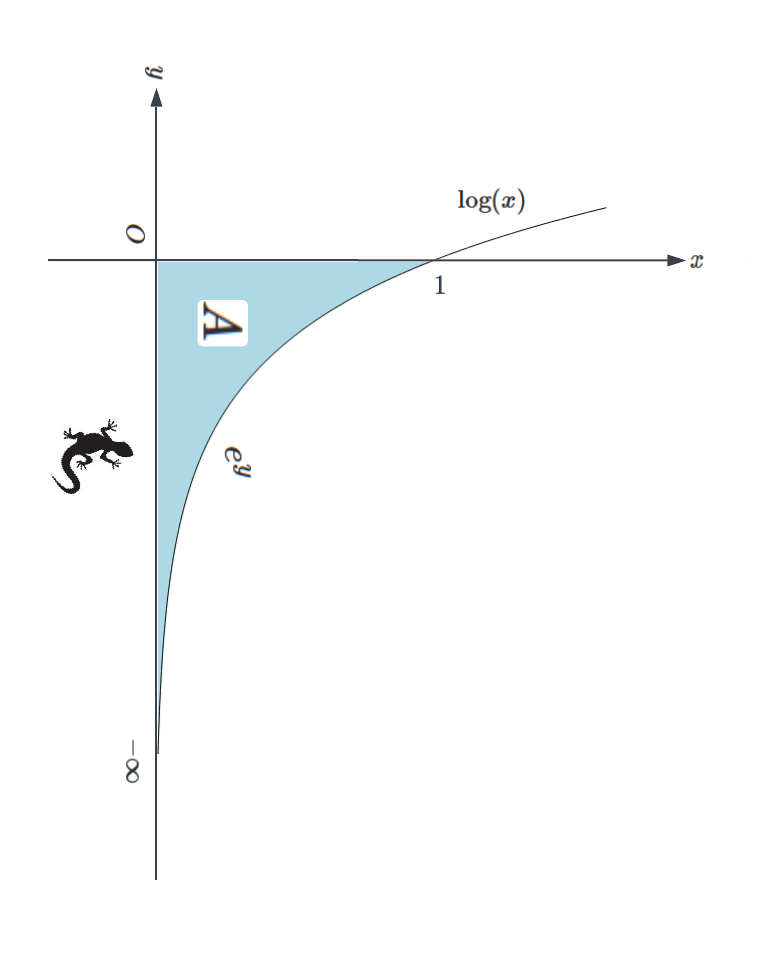

For
Let

I see and
Since for
I have
so
.


In a 1905 article, Charles-Ange Laisant, a French politician and mathematician, introduced the following theorem:
Given a function with inverse
, then
where is an arbitrary real constant.
It can also be stated equivalently as:
Given a function with inverse
then
where is an arbitrary real constant.
Moreover, this theorem gives
and
Frequently, obtaining an antiderivative for is relatively easier than finding one for
. In such instances, substituting the integrals of
with integrals involving
can be advantageous.
For example, let we have
As a result,
That is,
Another illuminating example is as follows:
Since we have
Prove
is an antiderivative of
Therefore,
Prove
By (2),
Prove
Exercise-1 Prove (2)
Exercise-2 Prove (3)
Exercise-3 What is
(Hint: )
Exercise-4 Explain and
Exercise-5 Show that (2) can be written as
And, prove
Exercise-6 Derive (1) (Hint: The foundation of a technique for evaluating definite integrals and Integration by Parts Done Right)

Prove:
For any positive number , let
Since is a monotonic increasing function:
we have
That is,
or
By the definition of :
we also have
Combining (1) and (2) gives
This implies that
In other words,
See also The Sandwich Theorem for Functions 2.

Evaluate
This integral is known as the Dirichlet Integral, named in honor of the esteemed German mathematician Peter Dirichlet. Due to the absence of an elementary antiderivative for the integrand, its evaluation by applying the Newton-Leibniz rule renders an impasse. However, the Feynman’s integral technique offers a solution.
The even nature of the function implies that
Let’s consider
and define
We can differentiate with respect to
Hence, we find
Integrating with respect to from
to
gives
Since
and
,
we arrive at
It follows that by (*):
Show that
From the inequality
and
(see (3) in A Proof without Calculus),
we deduce that
That is,
By the Sandwich Theorem for Functions 2,
Consequently,
Show that
That is,
Therefore,
Exercise-1 Evaluate by the schematic method (hint: Schematic Integration by Parts)

For given functions and
The given condition gives
and
It means
Since we have
That is,
Or,
And so,

See also Sandwich Theorems and Their Proofs.
Exercise-1 Prove
(Hint: )

Show that
This integral is renowned in mathematics as the Gaussian integral. Its evaluation poses a challenge due to the absence of an elementary antiderivative expressed in standard functions. Conventionally, one method involves “squaring the integral” and subsequently interpreting the resulting double integral in polar coordinates. However, an alternative approach, which we present here, employs Feynman’s integral technique.
The even nature of the function implies that
Let’s consider
and define
We can differentiate with respect to
Given a differentiable function on
with derivate
, the expression can be written as
Hence, we find
Integrating with respect to from
to
gives
Since
and
,
we arrive at
It follows that by (*):

From the inequality
we deduce that is a finite number.
As a result,
Excercise-1 Show that

Given is continuous on
and
satisfies the following conditions:
[1]
[2]
[3] has continuous derivative on
Prove:
The given premises
is a continuous function on
ensures the existence of the definite integral and the antiderivative of
Denoting the antiderivative of as
we obtain
We also deduce from [3] that
is continuous on
Combining [3], [1] and (1),
is continuous on
Additionally, as per [3],
is continuous on
Together, (4) and (5) give
is continuous on
Consequently, exists as well.
Now let’s examine , where
. We have
is the antiderivative of
This theorem serves as the foundation of a technique widely employed in evaluating definite integrals. By selecting a suitable substitution, the definite integral is transformed into a form that is more manageable or matches a known solution. This method proves particularly valuable for evaluating definite integrals involving complex functions or expressions.
For Example, to evaluate integral
,
we choose the following substitution for variable :
Since we can rewrite the integral as:
and proceed to evaluate the new integral as follows:
Let’s verify the result:
Suppose . Then
By Newton-Leibniz rule,
For grins, we also verify as follows:
That is,
Integrate it from to
,
Let we obtain
From “Deriving Two Inverse Functions“, we see that Therefore,
Now, letting we have
and
becomes
(see “Integral: I vs. CAS“)
Exercise-1
Exercise-2 (Hint: Consider
)