Newton’s Pi

/ Michael Xue

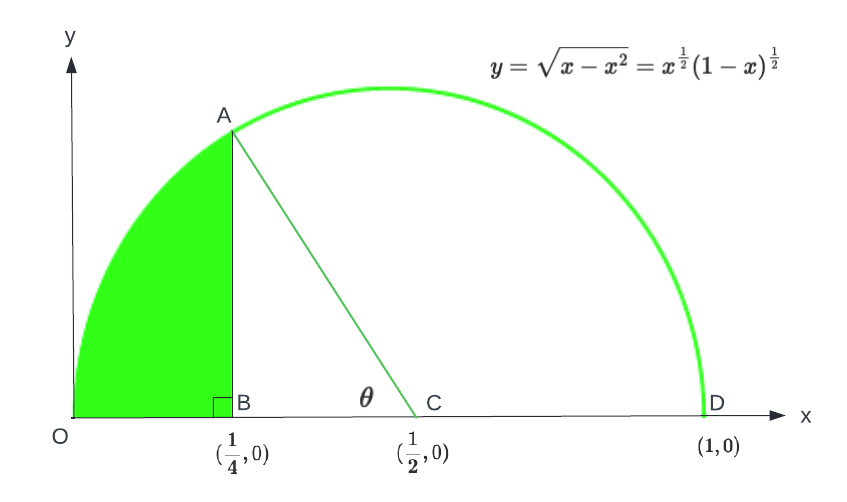
Fig. 1

Shown in Fig. 1 is a semicircle centered at C (\frac{1}{2}, 0) with radius = \frac{1}{2}. Its equation is

(x-\frac{1}{2})^2+y^2=(\frac{1}{2})^2, 0 \le x \le 1, y \ge 0.

Simplifying and solving for y gives

y = x^{\frac{1}{2}}\cdot(1-x)^{\frac{1}{2}}.\quad\quad\quad(1)

We see that

Area (sector OAC) = Area (sector OAB) + Area (triangle ABC).\quad\quad(*)

And,

a = BC = \frac{1}{2}-\frac{1}{4} = \frac{1}{4}, \quad\quad h = AB = \sqrt{AC^2-BC^2} = \sqrt{\frac{1}{2} - \frac{1}{4}}=\frac{\sqrt{3}}{2}.

It means

Area (triangle ABC) = \frac{1}{2}ah =\frac{1}{2}\cdot\frac{1}{4}\cdot\frac{\sqrt{3}}{4} = \frac{\sqrt{3}}{32}.\quad\quad\quad(2)

Moreover,

\cos(\theta) = \frac{BC}{AC} = \frac{\frac{1}{4}}{\frac{1}{2}} = \frac{1}{2} \implies \theta = \frac{\pi}{3}.

Since \theta is one-third of the \pi angle forming the semicircle, the sector is likewise a third of the semicircle. Namely,

Area (sector OAC) = \frac{1}{3} Area (semicircle) = \frac{1}{3} \cdot \frac{1}{2} \pi (\frac{1}{2})^2 = \frac{\pi}{24}.\quad\quad\quad(3)

Area (sector OAB) is the area under the curve y=x^{\frac{1}{2}}\cdot(1-x)^{\frac{1}{2}} from its starting point 0 to the point x=\frac{1}{4}. i.e.,

Area (sector OAB)

= \int\limits_{0}^{\frac{1}{4}}x^{\frac{1}{2}}\cdot(1-x)^{\frac{1}{2}}\;dx

= \int\limits_{0}^{\frac{1}{4}}x^{\frac{1}{2}}\cdot((-x)+1)^{\frac{1}{2}}\;dx

By the extended binomial theorem: (x+y)^r=\sum\limits_{i=0}^{\infty }x^iy^{r-i}, x, y, r \in R, |x|< |y| (see “A Gem from Isaac Newton“)

= \int\limits_{0}^{\frac{1}{4}}x^{\frac{1}{2}}\sum\limits_{i=0}^{\infty}\binom{\frac{1}{2}}{i}(-x)^i\;dx

=\int\limits_{0}^{\frac{1}{4}}x^{\frac{1}{2}}\sum\limits_{i=0}^{\infty}\binom{\frac{1}{2}}{i}(-1)^ix^i\;dx

= \int\limits_{0}^{\frac{1}{4}}\sum\limits_{i=0}^{\infty}\binom{\frac{1}{2}}{i}(-1)^ix^{\frac{2i+1}{2}}\;dx

= \sum\limits_{i=0}^{\infty}\binom{\frac{1}{2}}{i}(-1)^i\int\limits_{0}^{\frac{1}{4}}x^{\frac{2i+1}{2}}\;dx

=\sum\limits_{i=0}^{\infty}\binom{\frac{1}{2}}{i}(-1)^i\frac{2}{2i+3}x^{\frac{2i+3}{2}}\bigg|_{0}^{\frac{1}{4}}

x=\frac{1}{4} \implies x^{\frac{2i+3}{2}} simplifies beautifully: \left(\sqrt{\frac{1}{4}}\right)^{2i+3}=\left(\frac{1}{2}\right)^{2i+3}.

=\sum\limits_{i=0}^{\infty}\binom{\frac{1}{2}}{i}(-1)^i\frac{2}{2i+3}(\frac{1}{2})^{2i+3}

=\sum\limits_{i=0}^{\infty}\binom{\frac{1}{2}}{i}\frac{1}{4(2i+3)}(-\frac{1}{4})^i.\quad\quad\quad(4)

Expressing (*) by (3), (2) and (4), we have

\frac{\pi}{24}=\sum\limits_{i=0}^{\infty}\binom{\frac{1}{2}}{i}\frac{(-1)^i}{4^{i+1}(2i+3)}+\frac{\sqrt{3}}{32}.

Therefore,

\pi=24\left(\sum\limits_{i=0}^{\infty}\binom{r}{i}\frac{(-1)^i}{4^{i+1}(2i+3)}+\frac{\sqrt{3}}{32}\right).\quad\quad\quad(5)

Observe first that

\sqrt{3} = \sqrt{4-1} = \sqrt{4(1-\frac{1}{4})}=2\sqrt{1-\frac{1}{4}}=2\sqrt{\frac{-1}{4}+1}=2(\frac{-1}{4}+1)^{\frac{1}{2}}

and so we replace (\frac{-1}{4}+1)^{\frac{1}{2}} by its binomial expansion. As a result,

\sqrt{3} = 2\sum\limits_{i=0}^{\infty}\binom{\frac{1}{2}}{i}(-\frac{1}{4})^i.\quad\quad\quad(6)

Substituting (6) into (5) then yields

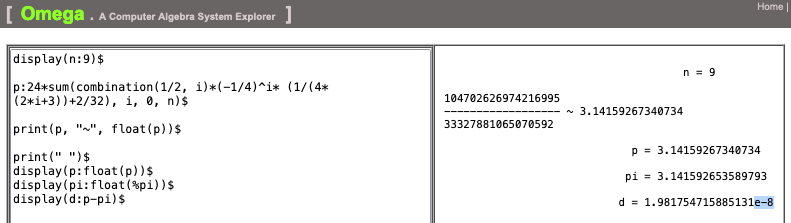
\pi = \sum\limits_{i=0}^{\infty}\binom{\frac{1}{2}}{i}\left(-\frac{1}{4}\right)^i\left(\frac{1}{4(2i+3)} + \frac{2}{32}\right).

Fig. 2 shows that with just ten terms (0 to 9) of the binomial expression, we have found \pi correct to seven decmal places.

Fig. 2

Leave a comment