
In Deriving the Extraordinary Euler Sum , we derived one of Euler’s most celebrated results:
Now, we aim to provide a rigorous proof of this statement.
First, we expressed the partial sum of the left-hand side as follows:
This splits the partial sum into two parts: one involving the squares of even numbers and the other involving the squares of odd numbers. Simplifying the even part gives us:
Rearranging terms on one side, we obtain:
Since converges to
(see My Shot at Harmonic Series)
converges to
to prove (1), it suffices to demonstrate that
or equivalently,

Let and
we have
and
Differentiating with respect to
That is,
Integrating with respect to from
to
and expressing the integrand in partial fractions:

yields
i.e.,
By (3) and (4),
or
which is (2)

Prove
Since
means
we have
Expand into its Maclaurin series:
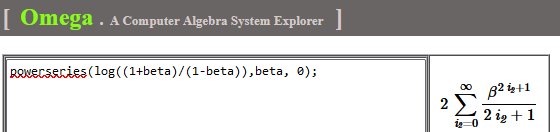
Prove
For
We have
As a result,
i.e.,
Moreover,
Let and
gives
It follows that